Question

If $P\left( x,y \right)$ is any point on the line joining the points $A\left( a,0 \right)$ and $B\left( 0,b \right)$ then show that $\dfrac{x}{a}+\dfrac{y}{b}=1$

Answer 1

In this type of question we have to use the concept of a straight line. We know that if the point lies on the same line then they are said to be collinear points. Also if $P\left( x,y \right)$ is a point lying on a straight line which joins the points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ then the equation of line is given by,
$\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.

Complete step-by-step solution:
Now, we have to prove $\dfrac{x}{a}+\dfrac{y}{b}=1$, if $P\left( x,y \right)$ is any point on the line joining the points $A\left( a,0 \right)$ and $B\left( 0,b \right)$
We know that, if $P\left( x,y \right)$ is a point lying on a straight line which joins the points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{2}},{{y}_{2}} \right)$ then the equation of line is given by, $\dfrac{y-{{y}_{1}}}{x-{{x}_{1}}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.

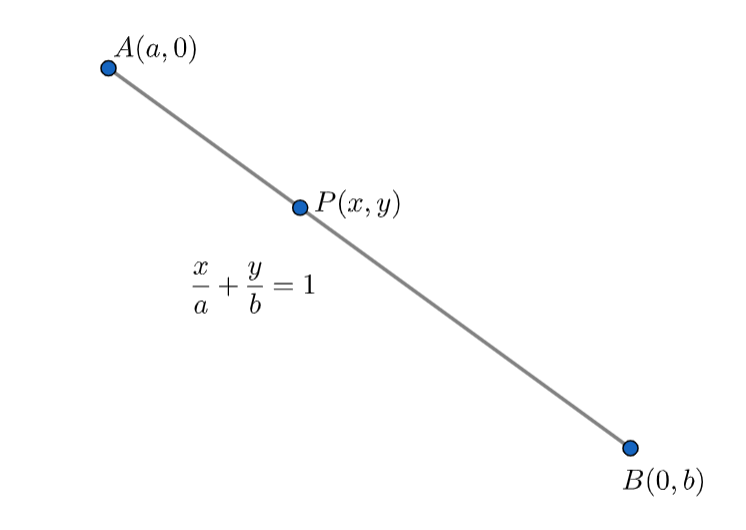
We have given that $P\left( x,y \right)$ is any point on the line joining the points $A\left( a,0 \right)$ and $B\left( 0,b \right)$.
Hence, by substituting the points $\left( {{x}_{1}},{{y}_{1}} \right)=\left( a,0 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,b \right)$ we can write the equation of the line as,

& \Rightarrow \dfrac{y-0}{x-a}=\dfrac{b-0}{0-a} \\\ & \Rightarrow \dfrac{y}{x-a}=-\dfrac{b}{a} \\\ \end{aligned}$$ Now, by performing cross multiplication and simplifying the equation we can write $$\begin{aligned} & \Rightarrow ay=-b\left( x-a \right) \\\ & \Rightarrow ay=-bx+ab \\\ & \Rightarrow bx+ay=ab \\\ \end{aligned}$$ Dividing both sides by $$ab$$ we get, $$\begin{aligned} & \Rightarrow \dfrac{bx}{ab}+\dfrac{ay}{ab}=\dfrac{ab}{ab} \\\ & \Rightarrow \dfrac{x}{a}+\dfrac{y}{b}=1 \\\ \end{aligned}$$ Hence proved Thus, if $$P\left( x,y \right)$$ is any point on the line joining the points $$A\left( a,0 \right)$$ and $$B\left( 0,b \right)$$ then the equation of line is given by $$\dfrac{x}{a}+\dfrac{y}{b}=1$$. **Note:** In this type of question students have to remember the formula of the equation of the line passing through a point. Students have to take care when they find the equation of the line; they have to substitute the values of $${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}$$ carefully to obtain the correct result. Also students have to take care when they obtain the final result; they have to remember to divide the equation $$bx+ay=ab$$ by $$ab$$.