Question

If $P\left( {{t}^{2}},2t \right)$, $t\in [0,2]$, is an arbitrary point on the parabola ${{y}^{2}}=4x$, Q is the foot of the perpendicular from the focus S on the tangent at P, then maximum area of $\Delta$ PQS is
(a) 1
(b) 2
(c) $\dfrac{5}{16}$
(d) 5

Answer 1

We will first find the tangent equation and then find the foot of the perpendicular on it. So we have all the three points and they form a right angled triangle as they mentioned “perpendicular”. So we can find the height and the length of the base. Finally we will just apply the $\dfrac{1}{2}bh$ formula and get the area. Then we will see its behavior in the interval [0, 2] and find its maximum.

Complete step-by-step answer :
First let us have a look at the diagram.

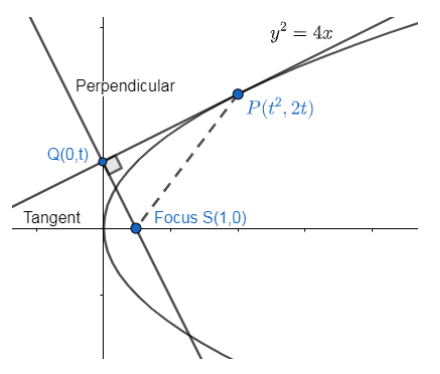
Now we know the point$P\left( {{t}^{2}},2t \right)$. Let us find the equation of the tangent at that point.
Let the equation of the tangent be $y=mx+c$.
Now let us find the slope m.
Given equation of the curve is,
${{y}^{2}}=4x$
$\Rightarrow {{y}^{2}}-4x=0$
Differentiating with respect to x on both sides we get,

& 2y\dfrac{dy}{dx}-4=0 \\\ & \Rightarrow 2y\dfrac{dy}{dx}=4 \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{4}{2y} \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{2}{y} \\\ & \Rightarrow m=\dfrac{2}{y} \\\ \end{aligned}$$ Since $$\dfrac{dy}{dx}$$ is slope m. Now let us substitute the point $$P\left( {{t}^{2}},2t \right)$$ in the above equation. Therefore, $$\begin{aligned} & m=\dfrac{2}{2t} \\\ & \Rightarrow m=\dfrac{1}{t} \\\ \end{aligned}$$ Thus, the equation of the tangent becomes, $$y=\dfrac{1}{t}x+c$$ Now to find the constant c, substitute the point $$P\left( {{t}^{2}},2t \right)$$ in the equation of the tangent since the tangent passes through that point. Therefore, we get, $$\begin{aligned} & 2t=\dfrac{1}{t}{{t}^{2}}+c \\\ & \Rightarrow 2t=t+c \\\ & \Rightarrow t=c \\\ \end{aligned}$$ Thus the equation of the tangent on the given parabola at the point $$P\left( {{t}^{2}},2t \right)$$ is, $$y=\dfrac{1}{t}x+t$$ $$\Rightarrow \dfrac{1}{t}x-y+t=0$$ Now let us find the foot of the perpendicular from focus S. First, we need the co-ordinates of the focus S. General form of the parabola is $${{y}^{2}}=4ax$$, where (a, 0) is its focus. Comparing the given parabola with the general equation we get, $$a=1$$. Thus the co-ordinates of the focus are (1,0). Thus, we need to find the foot of the perpendicular from S (1, 0) to the tangent. How do we do that? First let us find the line perpendicular to the tangent and which is passing S (1, 0). To find the perpendicular line we exchange the coefficients of the x and y terms and then let the constant be k. Thus the equation of the perpendicular is, $$x+\dfrac{1}{t}y=k$$. Now it passes through the point (1, 0), substituting the point (1,0) in the equation we get, $$\begin{aligned} & 1+0=k \\\ & \Rightarrow k=1 \\\ \end{aligned}$$ Therefore, the equation of the perpendicular becomes, $$x+\dfrac{1}{t}y=1$$ Solving this line equation and the tangent equation, we get the foot of the perpendicular from S (1, 0). Solving these two, $$\begin{aligned} & \dfrac{1}{t}x-y+t=0..........\times t \\\ & x+\dfrac{1}{t}y-1=0..........\times 1 \\\ \end{aligned}$$ This gives us, $$\begin{aligned} & x-ty+{{t}^{2}}=0 \\\ & x+\dfrac{1}{t}y-1=0 \\\ \end{aligned}$$ Subtracting the like terms we get, $$\begin{aligned} & \left( -t-\dfrac{1}{t} \right)y+({{t}^{2}}+1)=0 \\\ & \Rightarrow ({{t}^{2}}+1)=\left( t+\dfrac{1}{t} \right)y \\\ & \Rightarrow ({{t}^{2}}+1)=\left( \dfrac{{{t}^{2}}+1}{t} \right)y \\\ \end{aligned}$$ Cancelling the like terms and cross-multiplying we get, y = t Now substituting y = t in the tangent equation we get the x co-ordinate. $$\dfrac{1}{t}x-y+t=0$$ $$\begin{aligned} & \Rightarrow \dfrac{1}{t}x-t+t=0 \\\ & \Rightarrow \dfrac{1}{t}x=0 \\\ & \Rightarrow x=0 \\\ \end{aligned}$$ Thus, the foot of the perpendicular has co-ordinates Q (0, t). Thus, we know the co-ordinates $$P\left( {{t}^{2}},\text{ }2t \right),\text{ }Q\left( 0,\text{ }t \right)$$ and S (1, 0) and these form a right angled triangle as there is a “perpendicular” line. The right angle is that the foot of the perpendicular that is Q. Now let us find the distance between the points P and Q and then between the points Q and S. Now, $$\begin{aligned} & PQ=\sqrt{{{\left( {{x}_{P}}-{{x}_{Q}} \right)}^{2}}+{{\left( {{y}_{P}}-{{y}_{Q}} \right)}^{2}}} \\\ & \Rightarrow PQ=\sqrt{{{\left( {{t}^{2}}-0 \right)}^{2}}+{{\left( 2t-t \right)}^{2}}} \\\ & \Rightarrow PQ=\sqrt{{{t}^{4}}+{{t}^{2}}} \\\ & \Rightarrow PQ=t\sqrt{{{t}^{2}}+1} \\\ \end{aligned}$$ Similarly, $$\begin{aligned} & SQ=\sqrt{{{\left( {{x}_{S}}-{{x}_{Q}} \right)}^{2}}+{{\left( {{y}_{S}}-{{y}_{Q}} \right)}^{2}}} \\\ & \Rightarrow SQ=\sqrt{{{\left( 1-0 \right)}^{2}}+{{\left( 0-t \right)}^{2}}} \\\ & \Rightarrow SQ=\sqrt{1+{{t}^{2}}} \\\ & \Rightarrow SQ=\sqrt{{{t}^{2}}+1} \\\ \end{aligned}$$ Now PQ becomes the base and SQ becomes the height. Thus, $$\begin{aligned} & Area=\dfrac{1}{2}PQ\times SQ \\\ & \Rightarrow Area=\dfrac{1}{2}t\sqrt{{{t}^{2}}+1}\times \sqrt{{{t}^{2}}+1} \\\ & \Rightarrow Area=\dfrac{1}{2}t\left( {{t}^{2}}+1 \right) \\\ & \Rightarrow Area=\dfrac{{{t}^{3}}+t}{2} \\\ \end{aligned}$$ Now as t ϵ [0, 2], Area becomes maximum at t = 2 because $${{t}^{3}}+t$$ would be increasing in that interval.  Thus putting t =2 in the area equation we get, $$\begin{aligned} & Area=\dfrac{2+{{2}^{3}}}{2} \\\ & \Rightarrow Area=\dfrac{2+8}{2} \\\ & \Rightarrow Area=\dfrac{10}{2} \\\ & \Rightarrow Area=5 \\\ \end{aligned}$$ Thus option(d) is correct. **Note** :There is a shortcut for finding the foot of the perpendicular. Let the co-ordinates of the foot of the perpendicular be (h, k) from the point (p,q) on the line $$ax+by+c=0$$. The formula is, $$\dfrac{h-p}{a}\text{ }=\text{ }\dfrac{k-q}{b}\text{ }=\dfrac{-\left( ap+bq+c \right)}{({{a}^{2}}+{{b}^{2}})}$$ This formula will save you a lot of time.