Question

If $P\left( {9a - 2,b} \right)$ divides line segment joining $A\left( {3a + 1, - 3} \right)$ and $B\left( {8a,5} \right)$ in the ratio $3:1$, find the values of $a$ and $b$.
A.$a = 1,b = - 1$
B.$a = 1,b = 3$
C.$a = \dfrac{{11}}{{19}},b = 3$
D.$a = \dfrac{{11}}{{19}},b = - 1$

Answer 1

Here, we will use section formula to find the required values. We will substitute the given coordinates and ratio in the section formula and solve for the respective coordinates on both the sides to find the required values.

Formula Used:
Section Formula: Coordinates of point$P = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}$, where $P$ is a point dividing the line segment , $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of the end points of the line segment respectively. Also, $m$and $n$ are the ratios in which the points have divided the line segment.

Complete step-by-step answer:
According to the question,
We are given a line segment $AB$ such that the coordinates of Point $A = \left( {3a + 1, - 3} \right)$ and the coordinates of point $B = \left( {8a,5} \right)$.
Now, there is a point $P$ having the coordinates $\left( {9a - 2,b} \right)$ which divides the line segment $AB$ in a given ratio.
It is given that point $P$ divides the line segment $AB$in the ratio $m:n = 3:1$.
So, we can depict this information as shown below:

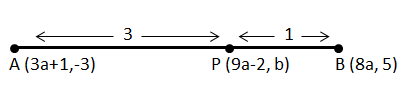
Now, substituting $\left( {{x_1},{y_1}} \right) = \left( {3a + 1, - 3} \right)$ , $\left( {{x_2},{y_2}} \right) = \left( {8a,5} \right)$ and the ratio $m:n = 3:1$ in the formula Coordinates of Point $P = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}$, we get,
Coordinates of point $P = \dfrac{{\left( 3 \right)\left( {8a} \right) + 1\left( {3a + 1} \right)}}{{3 + 1}},\dfrac{{\left( 3 \right)\left( 5 \right) + 1\left( { - 3} \right)}}{{3 + 1}}$
Multiplying the terms, we get
$\Rightarrow$ Coordinates of point $P = \dfrac{{24a + 3a + 1}}{4},\dfrac{{15 - 3}}{4}$
Adding and subtracting the like terms, we get
$\Rightarrow$ Coordinates of point $P = \dfrac{{27a + 1}}{4},\dfrac{{12}}{4}$
But it is given that coordinates of point $P = \left( {9a - 2,b} \right)$. Therefore,
$\Rightarrow \left( {9a - 2,b} \right) = \dfrac{{27a + 1}}{4},3$
Now, comparing the $x$ coordinates, we get
$9a - 2 = \dfrac{{27a + 1}}{4}$
On cross multiplication, we get
$\Rightarrow 36a - 8 = 27a + 1$
Adding and subtracting the like terms, we get
$\Rightarrow 9a = 9$
Dividing both sides by 9, we get
$\Rightarrow a = 1$
Also, comparing $y$ coordinates, we get,
$b = 3$
Hence, the required values of $a$ and $b$ are 1 and 3 respectively.
Therefore, if $P\left( {9a - 2,b} \right)$ divides line segment joining $A\left( {3a + 1, - 3} \right)$ and $B\left( {8a,5} \right)$ in the ratio $3:1$, then, $a = 1,b = 3$
Hence, option B is the correct answer.

Note: In this question, three points are given with their respective coordinates. We should take care while solving the question, that we substitute the correct coordinates in the correct place. For example, in the section formula, if we substitute $\left( {{x_1},{y_1}} \right)$ in such a way that the $x$ coordinate is of point $A$ and the $y$ coordinate is of point $B$. Then, our answer will be wrong. Similarly, while comparing the $x$ and $y$ coordinates we should keep in mind that we compare the respective coordinates on the respective sides, i.e. we should not compare $x$ coordinate in the LHS with $y$ coordinate in the RHS.