Question

If P is the point in the argand diagram corresponding to the complex number $\sqrt 3 + i$ and if $OPQ$ is an isosceles right angled triangle ,right angled at $O$, then $Q$ represents the complex number:

Answer 1

The argand diagram is used for graphical representation of complex numbers in the form of $x + iy$ in the complex plane. Similar to $x - axis$ and $y - axis$ in the two dimensional geometry we have a horizontal axis used to indicate real numbers and a vertical axis used to represent imaginary numbers in case of an argand plane. For example: $5 + 4i$ represents the ordered pair $\left( {5,4} \right)$ geographically in the argand plane.

Complete step-by-step solution:
The given complex number is; $P = \sqrt 3+i$
According to the given question, let us draw the diagram to understand the question in a better way;

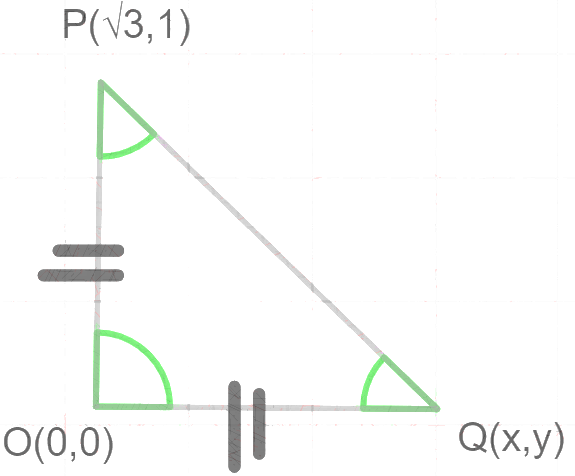
Figure $\left( 1 \right)$ : Isosceles right angled triangle $OPQ$
$\Rightarrow z = x + iy{\text{ }}\left( {{\text{Real part = }}x,{\text{ Imaginary part = }}y} \right)$
We know that if two lines are perpendicular to each other then the product of their slopes will be equal to $- 1$ ; i.e.
$\Rightarrow {m_1} \times {m_2} = - 1$
First, let us calculate the slope $\left( {{m_1}} \right)$ of line OP;
$\Rightarrow {m_1} = \left[ {\dfrac{{1 - 0}}{{\sqrt 3 - 0}}} \right] = \dfrac{1}{{\sqrt 3 }}{\text{ }}......\left( 1 \right)$
Now, let us calculate slope $\left( {{m_2}} \right)$ of line OQ;
$\Rightarrow {m_2} = \left[ {\dfrac{{y - 0}}{{x - 0}}} \right] = \dfrac{y}{x}{\text{ }}......\left( 2 \right)$
Put the respective values in the property ${m_1} \times {m_2} = - 1$ , we get;
$\Rightarrow \dfrac{1}{{\sqrt 3 }}{\text{ }} \times \dfrac{y}{x}{\text{ }} = - 1$
Simplifying the above equation;
$\Rightarrow y = - \sqrt 3 x{\text{ }}......\left( 3 \right)$
Using the properties of isosceles triangles (stated in the note part) let us try to solve our question;
According to figure $\left( 1 \right)$ , $OP = OQ{\text{ }}\left( {\because {\text{Congruent sides of the isosceles triangle}}} \right)$
$\therefore O{P^2} = O{Q^2}$ will also be true.
By the distance formula between two points, we know that;
$\Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$ ( where $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ are the coordinates of first
point and second point respectively )
$\Rightarrow O{P^2} = \left[ {\left( {{{\left( {\sqrt 3 } \right)}^2} - 0} \right) + \left( {{{\left( 1 \right)}^2} - 0} \right)} \right]$
$\Rightarrow O{P^2} = 3 + 1 = 4{\text{ }}......\left( 4 \right)$
Now, let us similarly find the equation for OQ;
$\Rightarrow O{Q^2} = \left[ {\left( {{{\left( x \right)}^2} - 0} \right) + \left( {{{\left( y \right)}^2} - 0} \right)} \right]$
$\Rightarrow O{Q^2} = {x^2} + {y^2}$
Now, put the value of $y = - \sqrt 3 x$ from equation $\left( 3 \right)$ in the above equation we get;
$\Rightarrow O{Q^2} = {x^2} + {\left( { - \sqrt 3 x} \right)^2}$
The above equation can be further simplified as;
$\Rightarrow O{Q^2} = {x^2} + 3{x^2}$
$\Rightarrow O{Q^2} = 4{x^2}{\text{ }}......\left( 5 \right)$
On comparing equation $\left( 4 \right)$ and equation $\left( 5 \right)$ , we get;
$\Rightarrow 4{x^2} = 4$
$\Rightarrow {x^2} = 1$
Which means ; $x = \pm 1$
Now put the value of $x{\text{ in equation }}\left( 3 \right)$ to get the value of $y$ ; we get two cases;
When $x = 1{\text{ , }}y = - \sqrt 3$
And $x = - 1{\text{ }}y = \sqrt 3$
Therefore, there can be two possible values of $Q$ , i.e. $Q\left( { \pm 1{\text{ }},{\text{ }} \mp \sqrt 3 } \right)$
Therefore, the answer for this question is $Q = 1 - \sqrt 3 i{\text{ or }}Q = - 1 + \sqrt 3 i$.

Note: Here are the important properties of a right angled isosceles triangle. It will be easier to understand via a diagram, the isosceles triangle theorem states that;

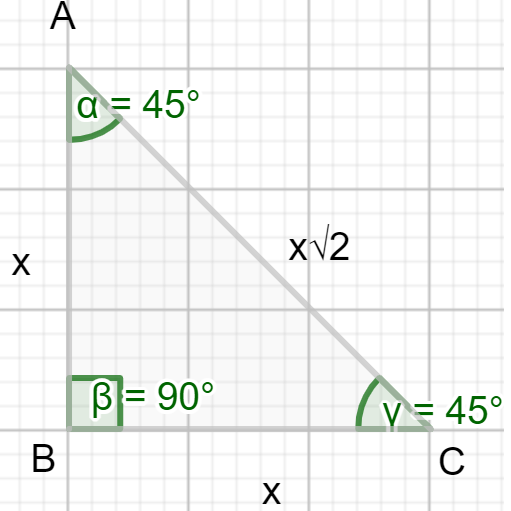
Figure $\left( 2 \right)$ : Isosceles triangle theorem
$\left( 1 \right)$ In the above diagram $AB = BC = X$ , means two sides of the triangle are congruent, then the third side will be equal to $X\sqrt 2$ means the hypotenuse is $\sqrt 2$ times the length of a leg.
$\left( 2 \right)$ If $AB = BC$ then $\angle BAC = \angle BCA$ .