Solveeit Logo
Login

Question

Question: If P is any point on the ellipse \[(\dfrac{{{x^2}}}{{36}}) + (\dfrac{{{y^2}}}{{16}}) = 1\]and\[\;S\]...

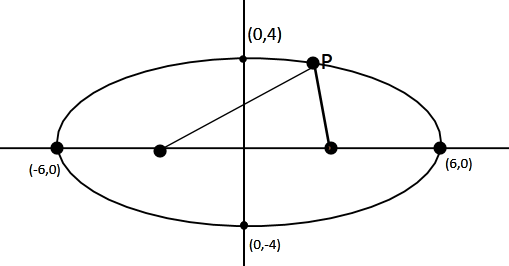
If P is any point on the ellipse (x236)+(y216)=1(\dfrac{{{x^2}}}{{36}}) + (\dfrac{{{y^2}}}{{16}}) = 1and  S\;S and S′S' are the foci, then PS + PS′ =PS{\text{ }} + {\text{ }}PS'{\text{ }} =
1)$$$4$ 2)8$ $$3)10 $$4)$$$12

Explanation

Solution

We have to find the value of sum of PSPS and PS′PS' . We solve this question using the concept of an ellipse . We should have the knowledge about the terms such as foci , vertex point and the centre point of the ellipse . We use the formula of focal distance of any point P on the ellipse . We should also have the concept of length of major axis and minor axis .

Complete step-by-step solution:
Given :
(x236)+(y216)=1(\dfrac{{{x^2}}}{{36}}) + (\dfrac{{{y^2}}}{{16}}) = 1
We know that the general equation of ellipse is given by :-
(x−h)2a2+(y−k)2b2=1\dfrac{{{{(x - h)}^2}}}{{{a^2}}} + \dfrac{{{{(y - k)}^2}}}{{{b^2}}} = 1
Where a and b are the length of major axis and minor axis respectively ( a > b ) . (h , k)\left( {{\text{ }}a{\text{ }} > {\text{ }}b{\text{ }}} \right){\text{ }}.{\text{ }}\left( {h{\text{ }},{\text{ }}k} \right) are the centre point of the ellipse .
Comparing the two equations , we compute that a2=36,b2=16,h=0{a^2} = 36,{b^2} = 16,h = 0 and k = 0k{\text{ }} = {\text{ }}0 .
The centre point of the ellipse is (0 , 0)\left( {0{\text{ }},{\text{ }}0} \right) .
The length of major axis = 6 units = {\text{ }}6{\text{ }}units
The length of minor axis = 4 units = {\text{ }}4{\text{ }}units
Point of foci of an ellipse is ( ± c , 0 )\left( {{\text{ }} \pm {\text{ }}c{\text{ }},{\text{ }}0{\text{ }}} \right)
The formula for calculating the foci is c=[a2−b2]c = \sqrt {[{a^2} - {b^2}]}
The point of foci of the ellipse =(±[36−16],0) = ( \pm \sqrt {[36 - 16]} ,0)
The point of foci of the ellipse =(±25,0) = ( \pm 2\sqrt 5 ,0)
The sum of distance of a point P on the ellipse from the foci is equal to twice the length of the major axis .
So ,
PS + PS′ = 2 × 6PS{\text{ }} + {\text{ }}PS'{\text{ }} = {\text{ }}2{\text{ }} \times {\text{ }}6
PS + PS′ = 12 unitsPS{\text{ }} + {\text{ }}PS'{\text{ }} = {\text{ }}12{\text{ }}units
Thus , the sum of distance of point PP from the foci SS and S′S' is 12 units12{\text{ }}units .
Hence , the correct option is (4)\left( 4 \right)

Note: An ellipse is the set of all points in a plane , the sum of whose distance from two fixed points in the plane is a constant . The Latus Rectum of an ellipse is a line segment perpendicular to the major axis through any of the foci and whose endpoints lie on the ellipse . Length of the Latus Rectum of the ellipse (x2a2)+(y2b2)=1(\dfrac{{{x^2}}}{{{a^2}}}) + (\dfrac{{{y^2}}}{{{b^2}}}) = 1 is 2×(b2a)2 \times (\dfrac{{{b^2}}}{a}) .