Question

If $P$ is a point on the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$ whose foci are $S$ and $S'$ , then $PS + PS' = 8$ .

Answer 1

Some of the properties of an ellipse that we need to know before getting into this problem: For an ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , the sum of the distance of a point on the ellipse from the two foci will be equal to the length of major axis that is $2b$ . On find the length of major axis we can compare and find whether the given statement is true or false.

Complete Step by step answer:
It is given that P is a point on the ellipse $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$ . The foci of this ellipse are $S$ and $S'$ .

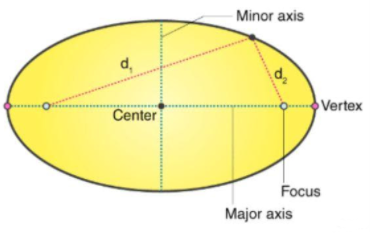
We aim is to verify that, $PS + PS' = 8$ which is nothing but the sum of the focal distance from a moving point $P$.
The given ellipse equation is $\dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{25}} = 1$ . We know that the general equation of an ellipse is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ . Thus, we get ${a^2} = 16$ and ${b^2} = 25$ .
Now let us find the values of $a$ & $b$ which we will be using later.
We have ${a^2} = 16$ . Taking square root, we get $a = \pm 4$ .
Likewise, we have ${b^2} = 25$ . Taking square root, we get $b = \pm 5$ .
We know that the sum of the distance of a point on the ellipse from the two foci will be equal to the length of major axis that is $2b$ so, let us find the value of $2b$ first.
We know that the value of $b$ is $\pm 5$ . Since the measure of length cannot be negative, we take $b = 5$ .
Thus $2b = 2 \times 5 = 10$ .
Thus, the length of major axis is $10$ . By the statement that the sum of the distance of a point on the ellipse from the two foci will be equal to the length of major axis that is $2b$ , we have to get $PS + PS' = 10$ , but it is given that $PS + PS' = 8$ .
When we compare this, we get to know that the given $PS + PS' = 8$ is wrong.

Note:
This problem is given like a statement thus, we have to verify it. When we verified this problem, we came to know that the given result is wrong. In case the given result is wrong then, we have to find the correct result and re-write the statement.