Solveeit Logo
Login

Question

Question: If P be a point on the parabola \({y^2} = 3\left( {2x - 3} \right)\) and M is the foot of the perpen...

If P be a point on the parabola y2=3(2x−3){y^2} = 3\left( {2x - 3} \right) and M is the foot of the perpendicular drawn from P on the directrix of the parabola, then length of each side of an equilateral △\vartriangle SMP, where S is the focus of the parabola is:
A.2
B.4
C.6
D.8

Explanation

Solution

We will convert the given equation of parabola into a standard equation to find the vertex and focus of the parabola. We will use the formula of directrix as x = – a. Then, we will draw the figure and from it, we will calculate the sine function for calculating the sides of the equilateral triangle.

Complete step-by-step answer:
We are given a parabola y2=3(2x−3){y^2} = 3\left( {2x - 3} \right)and we are said that M is the foot of perpendicular which was drawn from a point P at parabola to the directrix of the parabola.
S is the focus of the parabola.
We need to find the length of the equilateral triangle SMP.
Let us convert the given equation of the parabola into the standard form as: y2 = 4ax
The equation is: y2=3(2x−3){y^2} = 3\left( {2x - 3} \right)
Taking 2 common from the bracket on the right hand side of the equation, we get
⇒y2=6(x−32)\Rightarrow {y^2} = 6\left( {x - \dfrac{3}{2}} \right)
Now, we can write 6 in terms of 4 as
⇒y2=4×32(x−32)\Rightarrow {y^2} = 4 \times \dfrac{3}{2}\left( {x - \dfrac{3}{2}} \right)
Comparing this equation with y2{y}^{2} = 4ax, we get
⇒\Rightarrowa = 32\dfrac{3}{2}
therefore, the vertex of the parabola will be at (32,0)\left( {\dfrac{3}{2},0} \right).
We know that the directrix of a parabola is given by x = – a.
∴\therefore x = −32 - \dfrac{3}{2}will be the directrix that means the directrix will lie at a distance of 32\dfrac{3}{2}to the left of the vertex. We will draw the perpendicular M from the point P on the parabola and then we will join the M and focus S of the parabola to obtain the equilateral triangle SMP.
The focus S will be at “a” distance to the right of the vertex of the parabola i.e., its coordinates will be (32+32,0)≡\left( {\dfrac{3}{2} + \dfrac{3}{2},0} \right) \equiv (3, 0).

The figure of this arrangement will be:

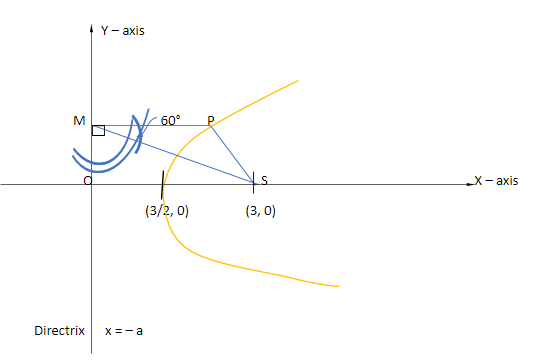
From the graph, we can see that if the triangle SMP is an equilateral triangle, then ∠\angle PMS will be 60°. Therefore, ∠\angle SMO will be 90° – 60° = 30°.
Now, in the right angle triangle MOS, applying sine function, we get
⇒sin⁡(∠OMS)=perpendicularhypotenuse\Rightarrow \sin (\angle OMS) = \dfrac{{perpendicular}}{{hypotenuse}}
⇒sin⁡30∘=OSSM\Rightarrow \sin {30^ \circ } = \dfrac{{OS}}{{SM}}
Putting the value of OS = 3, we get
⇒sin⁡30∘=3SM ⇒12=3SM ⇒SM=6  \Rightarrow \sin {30^ \circ } = \dfrac{3}{{SM}} \\\ \Rightarrow \dfrac{1}{2} = \dfrac{3}{{SM}} \\\ \Rightarrow SM = 6 \\\
Therefore, we get the length of the equilateral triangle as 6 units.
Hence, option (C) is correct.

Note: In such questions, you may get confused while reducing the given equation of the parabola into a standard equation. You may go wrong when selecting the method to proceed with in case of calculation of the length of the triangle and as well as while plotting the graph because you need to calculate everything beforehand like directrix, vertex and focus.