Question

If $\overrightarrow {AB} = 3i - 4j - k,\overrightarrow {BC} = 4i - j + 3k$ are two sides of $\Delta ABC$, then the angles of the triangles are?
${\text{A) }}A{\text{ = }}{90^ \circ },B = {45^ \circ },C = {45^ \circ } \\\ {\text{B) }}A{\text{ = 3}}{{\text{0}}^ \circ },B = {60^ \circ },C = {90^ \circ } \\\ {\text{C) }}A{\text{ = 4}}{{\text{5}}^ \circ },B = {60^ \circ },C = {75^ \circ } \\\ {\text{D) }}A{\text{ = 3}}{{\text{0}}^ \circ },B = {120^ \circ },C = {30^ \circ } \\\$

Answer 1

Start by drawing the triangle depicting the two sides with their vectors , using these two vectors find out the third vector . Apply the formula of dot product and find out the angle between any two vectors. Also pay attention to their direction as angle is measured only between two heads or two tails and not between head and tail. Similarly find out other angles as well.

Complete step-by-step answer :

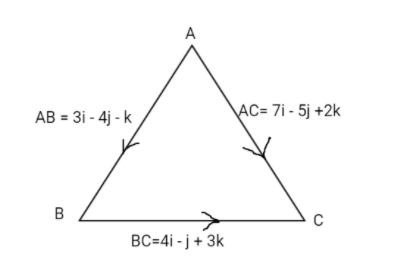
Given , $\overrightarrow {AB} = 3i - 4j - k \& \overrightarrow {BC} = 4i - j + 3k$
We have two sides in the form of vector , Let us try to find out the third side by using triangle law of vector addition as shown below

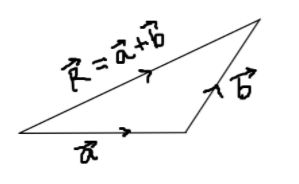
So , we can obtain side AC by adding the other two sides , by following the above rule for vector addition.
$\therefore \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \\\ \Rightarrow \overrightarrow {AC} = (3i - 4j - k) + (4i - j + 3k) \\\ \therefore \overrightarrow {AC} = 7i - 5j + 2k \\\$
Now that we have all the sides of the triangle , we can find the angle between any two sides of the triangles.
We know that angle between two vectors can be found using the formula
$\cos \theta = \dfrac{{\overrightarrow a \cdot \overrightarrow b }}{{\left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right|}}$
Let us find the angle between side \overrightarrow {AB} {\text{ & }}\overrightarrow {CB} using the above formula.
But $\overrightarrow {CB} = - \overrightarrow {BC} = - 4i + j - 3k$
$\cos \theta = \dfrac{{\overrightarrow {AB} \cdot \overrightarrow {CB} }}{{\left| {\overrightarrow {AB} } \right|\left| {\overrightarrow {BC} } \right|}} \\\ \Rightarrow \cos \theta = \dfrac{{(3i - 4j - k) \cdot ( - 4i + j - 3k)}}{{\left| {3i - 4j - k} \right|\left| {4i - j + 3k} \right|}} \\\ \Rightarrow \cos \theta = \dfrac{{ - 12 - 4 + 3}}{{\sqrt {{3^2} + {{( - 4)}^2} + {{( - 1)}^2}} \sqrt {{{( - 4)}^2} + {{(1)}^2} + {{( - 3)}^2}} }} \\\$
Here we used the formula
$i \cdot i = j \cdot j = k \cdot k = 1 \\\ i \cdot j = j \cdot k = k \cdot i = 0 \\\$
Also, for any vector $\overrightarrow P = ai + bj + ck$, then $\left| P \right| = \sqrt {{a^2} + {b^2} + {c^2}}$
$\Rightarrow \cos \theta = \dfrac{{ - 13}}{{\sqrt {26} \sqrt {26} }} \\\ \therefore \cos \theta = \dfrac{{ - 1}}{2} \\\ \therefore \theta = {120^ \circ } \\\$
So , the angle between side AB and CB is ${120^ \circ }$.
Similarly, Angle between side AC and BC will be
$\cos \theta = \dfrac{{\overrightarrow {AC} \cdot \overrightarrow {BC} }}{{\left| {\overrightarrow {AC} } \right|\left| {\overrightarrow {BC} } \right|}} \\\ \Rightarrow \cos \theta = \dfrac{{(7i - 5j + 2k) \cdot (4i - j + 3k)}}{{\left| {7i - 5j + 2k} \right|\left| {4i - j + 3k} \right|}} \\\ \Rightarrow \cos \theta = \dfrac{{28 + 5 + 6}}{{\sqrt {{7^2} + {{( - 5)}^2} + {{(2)}^2}} \sqrt {{4^2} + {{( - 1)}^2} + {3^2}} }} \\\ \Rightarrow \cos \theta = \dfrac{{39}}{{\sqrt {78} \sqrt {26} }} \\\ \Rightarrow \cos \theta = \dfrac{{\sqrt 3 }}{2} \\\ \therefore \theta = {30^ \circ } \\\$
So , the angle between AC and BC is ${30^ \circ }$.
Now that we know two angles of the triangles ,we can find out the third angle by using the angle sum property of the triangle, which states that the sum of all interior angles is equal to 180.
Therefore, The third angle is equal to ${180^ \circ } - {120^ \circ } - {30^ \circ } = {30^ \circ }$
Therefore , the triangle is a right angled triangle with angles $A = {30^ \circ },B = {120^ \circ },C = {30^ \circ }$
So , option D is the correct answer.

Note : Formation of vector quantity from direction cosines or ratios must be known. Generally , mistakes are committed while doing either the cross or dot product of two vectors , so need to be done carefully. Strict vigilance is required while doing the vector addition and dot products, to the signs as well while multiplying .