Question

If $\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \,\& \,\overrightarrow d$ are the position vectors of the points A,B,C and D respectively in the three dimensional space and satisfy the relation $3\overrightarrow a - 2\overrightarrow b + \overrightarrow c - 2\overrightarrow d = 0$ then
a) A,B,C,D are coplanar vectors
b) The line joining the points B and D divide the line joining points A and C in the ratio 2:1
c) The line joining the points A and C divide the line joining points B and D in the ratio 3:1
d) The four vectors $\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \,\& \,\overrightarrow d$ are linearly dependent

Answer 1

Check every option one by one. For example if relation $p\overrightarrow a + q\overrightarrow b + r\overrightarrow c + s\overrightarrow d = 0$ is given then for coplanar $p + q + r + s = 0$. For the second and third use ratio formula.

Complete step-by-step answer:
Here according to the question there are four points A, B, C, D whose position vectors are $\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \,\& \,\overrightarrow d$ respectively.
i) So firstly let us check the first option where A, B, C, D are coplanar vectors.
So here we are given the relation $3\overrightarrow a - 2\overrightarrow b + \overrightarrow c - 2\overrightarrow d = 0$, and we need to check coplanarity that means whether all four points are in one plane or not.
So if we are given equation $p\overrightarrow a + q\overrightarrow b + r\overrightarrow c + s\overrightarrow d = 0$ where a,b,c,d are position vectors then if coefficient sum will become zero, then its lies in a single plane.
Here relation is given by $3\overrightarrow a - 2\overrightarrow b + \overrightarrow c - 2\overrightarrow d = 0$
So here the sum of coefficients is $3 - 2 + 1 - 2 = 0$
Sp A, B, C, D are coplanar.
Option A is correct.
Now let's check other option
Here it is given that
$3\overrightarrow a - 2\overrightarrow b + \overrightarrow c - 2\overrightarrow d = 0$
Upon arranging we get by $3\overrightarrow a + \overrightarrow c = 2\overrightarrow b + 2\overrightarrow d$
Now if we divide on both sides by four
$\dfrac{{3\overrightarrow a + \overrightarrow c }}{4} = \dfrac{{2\overrightarrow b + 2\overrightarrow d }}{4}$
We can write as $\dfrac{{3\overrightarrow a + \overrightarrow c }}{{3 + 1}} = \dfrac{{2\overrightarrow b + 2\overrightarrow d }}{{2 + 2}}$

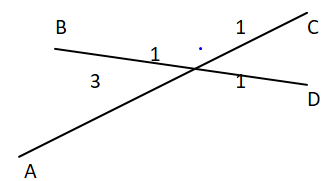
Here AC is divided into 1:3 ratio where BD is divided into 2:2 or 1:1 ratio.
ii) So the second option is wrong because it is saying that points B and D divide the line joining points A and C in the ratio 2:1 but here we get that BD divides AC in 1:3 ratio.
iii) Now, C option is correct as AC divides BD in 1:1 Ratio.
iv) If $\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \,\& \,\overrightarrow d$ are linearly independent then $p\overrightarrow a + q\overrightarrow b + r\overrightarrow c + s\overrightarrow d = 0$, if it is in this form where p, q, r and s are integers then they are linearly independent. So option D is incorrect.
So option A and C are correct.

Note: If three points are given then they are always coplanar, to determine a plane we must need 3 points. If four points are given and they are linearly independent and the sum of their coefficients is zero then these four points lie in the same plane that means coplanar.