Question

If $\overline a ,\overline b ,\overline c$ are position vectors of the vertices $A,B,C$ of $\Delta ABC.$ If $\overline r$ is the position vector of a point $P$ such that $\left( {\left| {\overline b - \overline c } \right| + \left| {\overline c - \overline a } \right| + \left| {\overline a - \overline b } \right|} \right)\overline r = \left| {\overline b - \overline c } \right|\overline a + \left| {\overline c - \overline a } \right|\overline b + \left| {\overline a - \overline b } \right|\overline c$ then the point $P$ is
A.Centroid of $\Delta ABC$
B.Orthocentre of $\Delta ABC$
C.Circumcentre of $\Delta ABC$
D.Incentre of $\Delta ABC$

Answer 1

Hint : For solving this particular question, we have to construct a triangle then we have to write the sides of the triangle in terms of position vector. After that we have to substitute the values in the given expression $\left( {\left| {\overline b - \overline c } \right| + \left| {\overline c - \overline a } \right| + \left| {\overline a - \overline b } \right|} \right)\overline r = \left| {\overline b - \overline c } \right|\overline a + \left| {\overline c - \overline a } \right|\overline b + \left| {\overline a - \overline b } \right|\overline c$ .

Complete step-by-step answer :
Let us consider a $\Delta ABC$ as shown in the given figure ,

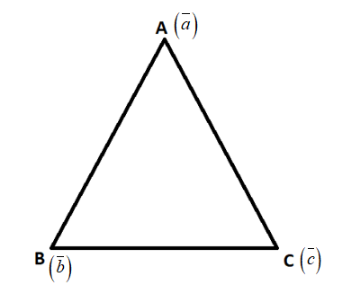
Here vertex ‘A’ of the above $\Delta ABC$ is equal to position vector $\overline a$ ,
vertex ‘B’ of the above $\Delta ABC$ is equal to position vector $\overline b$ , and
vertex ‘C’ of the above $\Delta ABC$ is equal to position vector $\overline c$ .
Now, the side ‘AB’ of the $\Delta ABC$ is equal to $\left| {\overline a - \overline b } \right|$ ,
the side ‘BC’ of the $\Delta ABC$ is equal to $\left| {\overline b - \overline c } \right|$ ,
the side ‘CA’ of the $\Delta ABC$ is equal to $\left| {\overline c - \overline a } \right|$ ,
It is given that $\overline r$ is the position vector of a point $P$ such that $\left( {\left| {\overline b - \overline c } \right| + \left| {\overline c - \overline a } \right| + \left| {\overline a - \overline b } \right|} \right)\overline r = \left| {\overline b - \overline c } \right|\overline a + \left| {\overline c - \overline a } \right|\overline b + \left| {\overline a - \overline b } \right|\overline c$
Now substitute the corresponding values, we will get ,

$$\Rightarrow \left( {\left| {\overline b - \overline c } \right| + \left| {\overline c - \overline a } \right| + \left| {\overline a - \overline b } \right|} \right)\overline r = \left| {\overline b - \overline c } \right|\overline a + \left| {\overline c - \overline a } \right|\overline b + \left| {\overline a - \overline b } \right|\overline c \\\ \Rightarrow (BC + CA + AB)\overline r = BC\overline a + CA\overline b + AB\overline c \\\ \Rightarrow \overline r = \dfrac{{BC\overline a + CA\overline b + AB\overline c }}{{(AB + BC + CA)}} \\\$$

where ‘AB’ , ‘BC’ , ‘CA’ represent the magnitude of the sides and $\overline a ,{\text{ }}\overline b {\text{ and }}\overline c$ are the position vectors of ‘A’, ‘B’ and ‘C’ points respectively.
Here if we compare the equation of $\overline r$ with the vector formula for incenter in a $\Delta PQR\;{\text{where}}\;\overline p ,\;\overline q \;{\text{and}}\;\overline r$ are position vectors of vertices $P,\;Q\;{\text{and}}\;R$ respectively is given as
Position vector of incenter $= \dfrac{{QR.\overline p + RP.\overline q + PQ.\overline r }}{{PQ + QR + RP}},\;{\text{where}}\;PQ,\;QR\;{\text{and}}\;RP$ are magnitude of sides,
So we can see that the above equation is matching with the formula for incenter of a triangle,
Therefore, we can say that point ‘P’ is the incenter
Then,
We can say that ‘D’ is the correct option.
So, the correct answer is “Option C”.

Note : We must know that for a point say $P$ to be Incentre we have the following expression ,
$\overline r = \dfrac{{AB\overline a + BC\overline b + CA\overline c }}{{(AB + BC + CA)}}$ . Where $\overline r$ is the position vector of point $P$ , where ‘AB’ , ‘BC’ , ‘CA’ represent the magnitude of the sides and $\overline a ,{\text{ }}\overline b {\text{ and }}\overline c$ are the position vectors of ‘A’, ‘B’ and ‘C’ points respectively and the denominator $AB + BC + CA$ is nothing but the perimeter of the given triangle.