Question

If orthocentre and circumcentre of triangle are respectively (1, 1) and (3, 2), then the co – ordinates of its centroid are: -
(a) $\left( \dfrac{7}{3},\dfrac{5}{3} \right)$
(b) $\left( \dfrac{5}{3},\dfrac{7}{3} \right)$
(c) (7, 5)
(d) None of these

Answer 1

Assume the co-ordinates of centroid of the triangle as (x, y). Apply the theorem that “centroid of a triangle divides the line joining its orthocentre and circumcentre in the ratio 2 : 1” and calculate the values of x and y using the section formula. Section formula is given as: - if a point (x, y) divides a line segment joining two points in the ratio m : n then, $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$ and $y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$, where $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the co – ordinates of two given points.

Complete step-by-step solution
Here, we have been provided with the coordinates of the orthocentre and circumcentre of the triangle and we have to find the coordinates of its centroid.
Now, we know that the centroid of a triangle divides its line joining the orthocentre and circumcentre into the ratio 2: 1. So, we have,

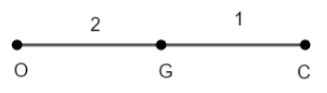
In the above figure we have denoted orthocentre with O, centroid with G and circumcentre with C. Therefore, we have according to the theorem,
$\Rightarrow OG:GC=2:1=m:n$
Now, we know that if a point (x, y) divides a line segment joining two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ in the ratio m : n then the co – ordinates x and y are given by the section formula: -
$\Rightarrow x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}$
$\Rightarrow y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$
Therefore, here in the above figure we have, co – ordinates of: -
(i) G = (x, y)
(ii) O = $\left( {{x}_{1}},{{y}_{1}} \right)$ = (1, 1)
(iii) C = $\left( {{x}_{2}},{{y}_{2}} \right)$ = (3, 2)
So, applying section formula, we get,

& \Rightarrow x=\dfrac{2\times 3+1\times 1}{2+1} \\\ & \Rightarrow x=\dfrac{7}{3} \\\ \end{aligned}$$ And, $$y=\dfrac{2\times 2+1\times 1}{2+1}$$ $$\Rightarrow y=\dfrac{5}{3}$$ Hence, co – ordinates of centroid, G = $$\left( \dfrac{7}{3},\dfrac{5}{3} \right)$$. **Therefore, option (a) is the correct answer.** **Note:** One may note that we cannot interchange the points of orthocentre and circumcentre. If we will do so then we have to change the ratio to 1: 2 from 2: 1. So, you must remember the order of the points. Remember the section formula so that the question can be easily solved. Here, we have assumed the points as O, G, and C, you may use different letters to denote them but the only important thing is their order and the ratio.