Question

If $\operatorname{Lim}_{x \rightarrow \infty} \left(\sqrt{A x^{2}+12 x}-B x\right)=3(A, B>0)$, then the value of (A+B), is

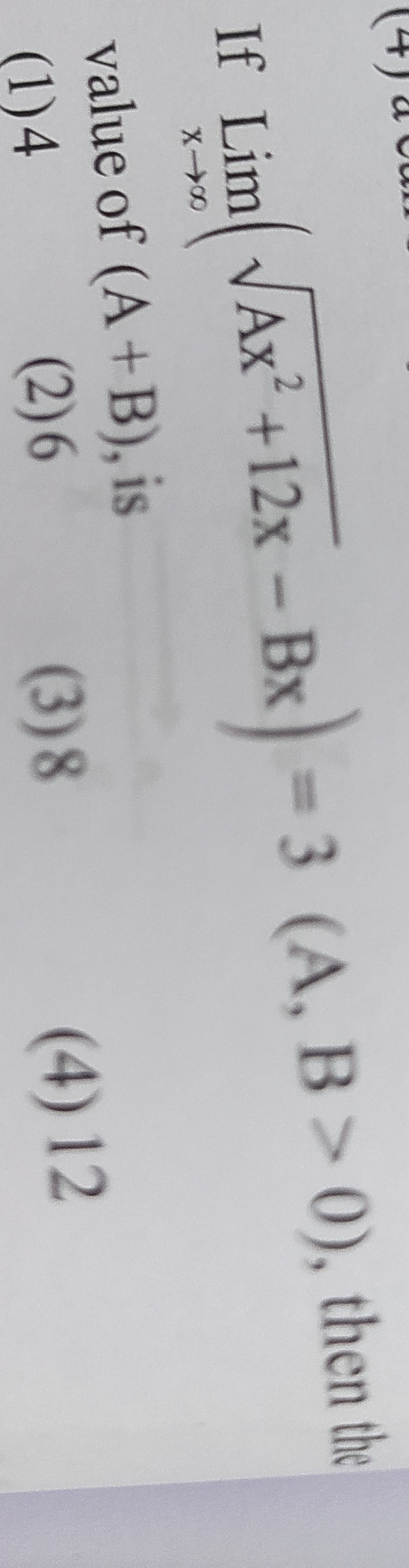
• A. 4
• B. 6
• C. 8
• D. 12

Answer 1

Answer: (B)

6

Answer 2

To find the value of A+B, given the limit condition, we proceed as follows:

1. Rationalize the expression:

   Multiply and divide by the conjugate:

   $$\operatorname{Lim}_{x \rightarrow \infty} \left(\sqrt{A x^{2}+12 x}-B x\right) = \operatorname{Lim}_{x \rightarrow \infty} \frac{(A - B^2) x^2 + 12 x}{\sqrt{A x^{2}+12 x}+B x}$$

2. Apply the limit condition:

   For the limit to be finite, $A - B^2 = 0$, implying $A = B^2$. This simplifies the limit to:

   $$\operatorname{Lim}_{x \rightarrow \infty} \frac{12 x}{\sqrt{A x^{2}+12 x}+B x}$$

   Divide both numerator and denominator by $x$:

   $$\operatorname{Lim}_{x \rightarrow \infty} \frac{12}{\sqrt{A + \frac{12}{x}} + B} = \frac{12}{\sqrt{A} + B}$$

3. Use the given limit value:

   Since the limit is equal to 3:

   $$\frac{12}{\sqrt{A} + B} = 3$$

   This simplifies to $\sqrt{A} + B = 4$.

4. Solve for A and B:

   Since $A = B^2$, substitute $B = \sqrt{A}$ into $\sqrt{A} + B = 4$:

   $$B + B = 4 \implies B = 2$$

   Then, $A = B^2 = 2^2 = 4$.

5. Calculate A+B:

   $$A + B = 4 + 2 = 6$$

Thus, the value of A+B is 6.