Solveeit Logo
Login

Question

Question: If OP = r, d.c’s of \[\overrightarrow{OP}\] are l, m and n then \(P=(lr,mr,nr)\)....

If OP = r, d.c’s of OP→\overrightarrow{OP} are l, m and n then P=(lr,mr,nr)P=(lr,mr,nr).

Explanation

Solution

To solve this question, we will first write the values of direction cosines in the Cartesian form. After that, we will find the length of line OP which passes through point P ( x, y z ) and origin. After that, we will substitute the value of length OP = r in values of direction cosines and hence obtain the coordinates of P in terms of cosines of line OP.

Complete step-by-step solution
Before we solve this question, let us see what direction cosines are.
In three – dimension geometry, we have three axes which are the x-axis, y-axis, and z-axis. Now, let us assume that line OP passes through the origin in the three – dimensional space. Then, it is obvious that the line will make an angle each with the x-axis, y-axis, and z-axis respectively.
Now, cosines of each of these three angles that the line makes with the x-axis, y-axis, and z-axis respectively are called direction cosines of the line in three-dimensional space. In general, these direction cosines are denoted by using letters l, m, and n.

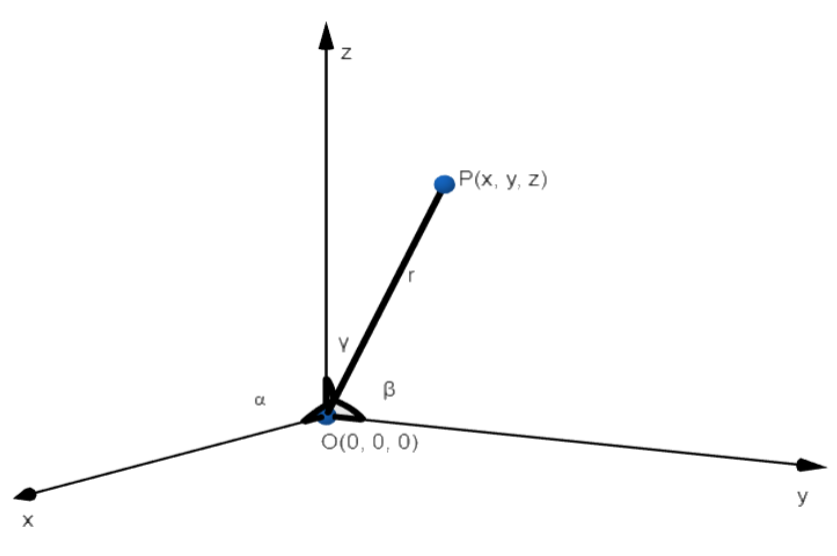
Now, we know that if l, m and n are direction cosines of a line passing through origin to point P(x, y, z), then l=xx2+y2+z2l=\dfrac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}} , m=yx2+y2+z2m=\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}, n=zx2+y2+z2n=\dfrac{z}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}
Now as OP passes from O( 0, 0, 0 ) and P( x, y, z )
So, using distance formula
OP=(x−0)2+(y−0)2+(z−0)2OP=\sqrt{{{(x-0)}^{2}}+{{(y-0)}^{2}}+{{(z-0)}^{2}}}
On simplifying, we get
OP=x2+y2+z2OP=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}
As, given that OP = r
So, r=x2+y2+z2r=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}
Substituting value of r=x2+y2+z2r=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}} in values of direction cosines, we get
l=xrl=\dfrac{x}{r} , m=yrm=\dfrac{y}{r}, n=zrn=\dfrac{z}{r}
Multiplying, both sides by r, we get
x = lr, y = mr and z = nr
Now, as (x, y, z ) are the coordinates of point P.
So, P ( lr, mr, nr )

Note: Always remember that if line passes through origin and point P ( x, y, z ) then direction cosines of line OP are equals to l=xx2+y2+z2l=\dfrac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}} , m=yx2+y2+z2m=\dfrac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}, n=zx2+y2+z2n=\dfrac{z}{\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}}. Also remember that length of line passing through points L( a, b, c ) and M( x, y, z ) is equals to LM=(x−a)2+(y−b)2+(z−c)2LM=\sqrt{{{(x-a)}^{2}}+{{(y-b)}^{2}}+{{(z-c)}^{2}}}. Try not to make any error while solving the question.