Question

If one root of the equation

$\begin{vmatrix} 7 & 6 & x^2-13 \\ 2 & x^2-13 & 2 \\ x^2-13 & 3 & 7 \end{vmatrix}$ = 0 is x = 2, the sum of all other five roots is

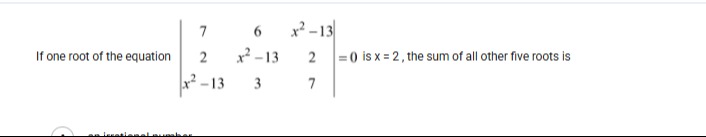
• A. -2
• B. 2
• C. 0
• D. -4

Answer 1

Answer: (A)

-2

Answer 2

The given equation is: $D = \begin{vmatrix} 7 & 6 & x^2-13 \\ 2 & x^2-13 & 2 \\ x^2-13 & 3 & 7 \end{vmatrix} = 0$

Let $y = x^2-13$. Substituting this into the determinant, we get: $D = \begin{vmatrix} 7 & 6 & y \\ 2 & y & 2 \\ y & 3 & 7 \end{vmatrix} = 0$

Expand the determinant along the first row: $7(7y - 2 \cdot 3) - 6(2 \cdot 7 - 2 \cdot y) + y(2 \cdot 3 - y \cdot y) = 0$ $7(7y - 6) - 6(14 - 2y) + y(6 - y^2) = 0$ $49y - 42 - 84 + 12y + 6y - y^3 = 0$ $-y^3 + (49+12+6)y - (42+84) = 0$ $-y^3 + 67y - 126 = 0$ Multiplying by -1, we get the cubic equation in $y$: $y^3 - 67y + 126 = 0$

The original equation is a polynomial in $x$. Since all occurrences of $x$ are in the term $x^2-13$, the expanded determinant will be a polynomial in $x^2$. Let $P(x)$ denote this polynomial. $P(x) = (x^2-13)^3 - 67(x^2-13) + 126$. When expanded, this will be a polynomial of the form $ax^6 + bx^4 + cx^2 + d = 0$. A key property of such a polynomial (where only even powers of $x$ are present) is that if $r$ is a root, then $-r$ is also a root. This is because $P(-r) = P(r)$. Therefore, the roots of $P(x)=0$ occur in pairs $(r_i, -r_i)$. For a sixth-degree polynomial, there will be six roots. Let them be $r_1, r_2, r_3, r_4, r_5, r_6$. Since the roots come in pairs $(k, -k)$, the sum of all roots will be: Sum of all roots $= r_1 + (-r_1) + r_2 + (-r_2) + r_3 + (-r_3) = 0$.

We are given that one root of the equation is $x=2$. Let this be $r_1=2$. The sum of all six roots is $0$. So, $2 + (\text{sum of other five roots}) = 0$. Therefore, the sum of all other five roots is $-2$.

To verify this, we can find all roots: Given $x=2$ is a root, $y = x^2-13 = 2^2-13 = 4-13 = -9$. Substitute $y=-9$ into the cubic equation: $(-9)^3 - 67(-9) + 126 = -729 + 603 + 126 = -729 + 729 = 0$. So, $y=-9$ is a root. This means $(y+9)$ is a factor of $y^3 - 67y + 126$. Using polynomial division or synthetic division: $(y^3 - 67y + 126) \div (y+9) = y^2 - 9y + 14$. So, $y^3 - 67y + 126 = (y+9)(y^2 - 9y + 14) = 0$. Factor the quadratic: $y^2 - 9y + 14 = (y-2)(y-7)$. Thus, the roots for $y$ are $y = -9, y = 2, y = 7$.

Now, we find the corresponding values of $x$ using $x^2-13 = y$:

1. If $y = -9$: $x^2 - 13 = -9 \implies x^2 = 4 \implies x = \pm 2$.
2. If $y = 2$: $x^2 - 13 = 2 \implies x^2 = 15 \implies x = \pm \sqrt{15}$.
3. If $y = 7$: $x^2 - 13 = 7 \implies x^2 = 20 \implies x = \pm \sqrt{20} = \pm 2\sqrt{5}$.

The six roots of the equation are $2, -2, \sqrt{15}, -\sqrt{15}, 2\sqrt{5}, -2\sqrt{5}$. The problem states that one root is $x=2$. The other five roots are $-2, \sqrt{15}, -\sqrt{15}, 2\sqrt{5}, -2\sqrt{5}$. The sum of these five roots is: $-2 + \sqrt{15} + (-\sqrt{15}) + 2\sqrt{5} + (-2\sqrt{5}) = -2 + 0 + 0 = -2$.

The final answer is -2.

Explanation of the solution:

1. Recognize that the determinant equation is a polynomial in $x^2$. Let $y = x^2-13$.
2. Expand the determinant to obtain a cubic equation in $y$: $y^3 - 67y + 126 = 0$.
3. Since the original equation is a polynomial in $x^2$, it means if $x_0$ is a root, then $-x_0$ is also a root.
4. This implies that all roots come in pairs $(k, -k)$.
5. Therefore, the sum of all six roots of the equation is $0$.
6. Given one root is $x=2$, the sum of the other five roots must be $0 - 2 = -2$.