Question

If one root of eq. $x^2-x+3a=0$ double the root of eq. $x^2-x+a=0$

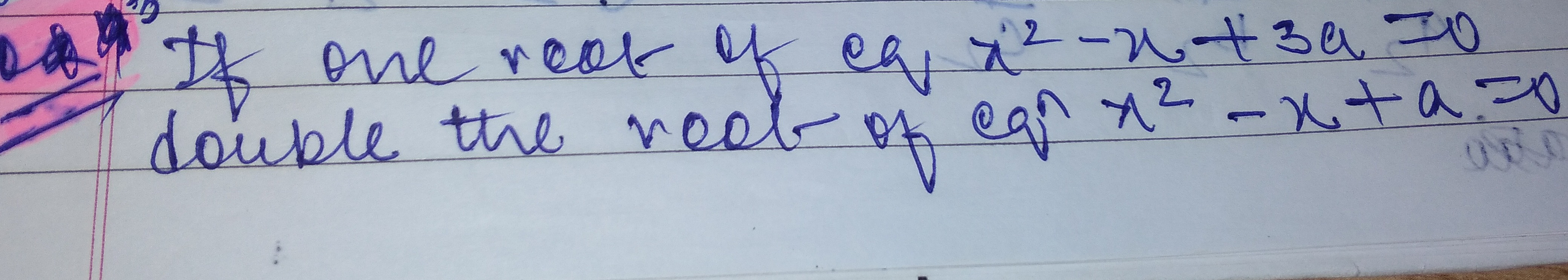
Answer 1

a=0 or a=-2

Answer 2

Let the roots of $x^2-x+a=0$ be $\alpha, \beta$ and the roots of $x^2-x+3a=0$ be $\gamma, \delta$. From Vieta's formulas, $\alpha+\beta=1, \alpha\beta=a$ and $\gamma+\delta=1, \gamma\delta=3a$. Assuming $\gamma=2\alpha$, we get $\beta=1-\alpha$ and $\delta=1-2\alpha$. Substituting into the product of roots equations: $\alpha(1-\alpha)=a$ and $(2\alpha)(1-2\alpha)=3a$. Eliminating $a$ yields $\alpha^2+\alpha=0$, so $\alpha=0$ or $\alpha=-1$. For $\alpha=0$, $a=0$. For $\alpha=-1$, $a=-2$. Both values are valid.