Question

If one of the vertices of the square circumscribing the circle $\left| z-1 \right|=\sqrt{2}$is $\left( 2+\sqrt{3}i \right)$. Find the other vertices of the square.
A.$\left( 1-\sqrt{3} \right)+2i$and $\left( 1+\sqrt{3} \right)-2i$
B.$\left( 1-\sqrt{3} \right)$and $\left( 1+\sqrt{3} \right)$
C.$\left( 1-\sqrt{3} \right)+i$and $\left( 1+\sqrt{3} \right)-i$
D.None of these

Answer 1

Hint: Find the center and radius of the circle and draw a rough figure. Take vertices of the square as ${{z}_{1}},{{z}_{2}},{{z}_{3}},{{z}_{4}}$. We know one vertex, take it as ${{z}_{1}}$and center ${{z}_{0}}$. By mid-point theorem find ${{z}_{2}}$. Using theorems of complex numbers, find ${{z}_{3}}$and ${{z}_{4}}$.

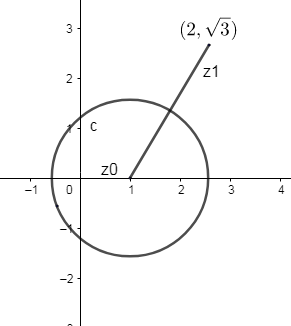
Given the circle $\left| z-1 \right|=\sqrt{2}$, which is the equation of a circle with center (1, 0). Thus it becomes the midpoint of the diagonal of the square. The radius of the circle is $\sqrt{2}$, as per the equation of the circle given.

The graphical representation of $\left| z-1 \right|=\sqrt{2}$in the complex plane is a circle of radius $\sqrt{2}$centered at point (1, 0).

The graphical representation of $\left( 2+i\sqrt{3} \right)$is at the point $\left( 2,\sqrt{3} \right)$where x = 2 and $y=\sqrt{3}$, which is of the form $x+iy$.

Now let us consider each vertex as ${{z}_{1}},{{z}_{2}},{{z}_{3}}$and ${{z}_{4}}$of the square to be formed. We know one vertex, let it be ${{z}_{1}}=2+i\sqrt{3}$.

Let us consider O as the center of the circle. We know the coordinates of the center of the circle as (1, 0) which form $1+0i$. We can mark it as ${{z}_{0}}$.

$\therefore {{z}_{0}}=1+0i$.
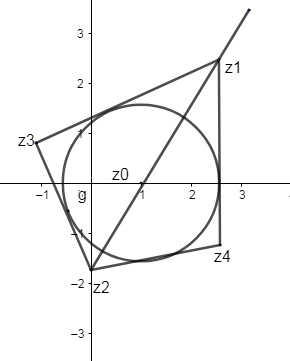
In case of a square, all sides are equal. They have the same magnitude and are located at ${{90}^{\circ }}$from each other. The diagonals of a square are of the same length and congruent. Therefore, by using mid-point theorem, we can find the vertex ${{z}_{2}}$, where we know the value of other vertex ${{z}_{1}}$and midpoint, which is the same as the center.

(Figure 1)

(Figure 2)
$\therefore \dfrac{{{z}_{1}}+{{z}_{2}}}{2}={{z}_{0}}$[From figure 2]
$\begin{aligned} & \therefore {{z}_{1}}+{{z}_{2}}=2{{z}_{0}} \\\ & {{z}_{2}}=2{{z}_{0}}-{{z}_{1}}=2\times 1-\left( 2+i\sqrt{3} \right)=-\sqrt{3}i \\\ & \therefore {{z}_{2}}=0-\sqrt{3}i \\\ \end{aligned}$
A complex number is perpendicular to another complex number, ${{r}^{ei\theta }}$which is represented by ${{r}^{ei\left( \theta +\dfrac{\pi }{2} \right)}}$, where the $\theta$is the angle made by the complex number with the x-axis
$\because \cos \dfrac{\pi }{2}=1$
$\Rightarrow \sin \dfrac{\pi }{2}=0$
$\left[ {{e}^{\pm \dfrac{\pi }{2}}}=\cos \dfrac{\pi }{2}\pm i\sin \dfrac{\pi }{2} \right]$
Now let us consider the vertex ${{z}_{1}}$and ${{z}_{3}}$,
$\begin{aligned} & \dfrac{{{z}_{4}}-1}{{{z}_{1}}-1}={{e}^{\pm i\dfrac{\pi }{2}}} \\\ & {{z}_{4}}-1=\left( {{z}_{1}}-1 \right){{e}^{\pm i\dfrac{\pi }{2}}} \\\ & {{z}_{4}}-1=\left( 2+i\sqrt{3}-1 \right)\left( \cos \dfrac{\pi }{2}\pm i\sin \dfrac{\pi }{2} \right) \\\ & \Rightarrow {{z}_{4}}=\left( 1+i\sqrt{3} \right)\left( i\sin \dfrac{\pi }{2} \right)+1 \\\ & {{z}_{4}}=i\left( 1+i\sqrt{3} \right)+1 \\\ & {{z}_{4}}=i-\sqrt{3}+1 \\\ \end{aligned}$
Hence, we got the required vertex of square as,
${{z}_{2}}=0-\sqrt{3}i,{{z}_{3}}=\left( 1-\sqrt{3}+i \right)$and ${{z}_{4}}=\left( 1+\sqrt{3}-i \right)$.
$\therefore$Vertices of square are $\left( 1-\sqrt{3},1 \right),\left( 0,-\sqrt{3} \right)$and $\left( 1+\sqrt{3},-1 \right)$.
Hence, option (c) is the correct answer.
Note:
Some complex numbers have absolute value 1. For a unit circle of radius 1 at centered at O. It includes all complex numbers of absolute value 1, which has the equation as $\left| z \right|=1$, where $z=x+iy$. In a question like this remember the properties of squares and circles which indulge in complex numbers.