Question

If one of the lines of the pair $a{{x}^{2}}+2bxy+b{{y}^{2}}=0$ bisects the angle between x-axis and y-axis, then
[a] a+b = 12b
[b] a+b = -2b
[c] a+b = 2b
[d] ${{\left( a-b \right)}^{2}}=4{{b}^{2}}$

Answer 1

Hint: Use the fact that the pair of straight lines represented by the homogeneous equation $a{{x}^{2}}+2hxy+c{{y}^{2}}=0$ pass through the origin. Use the fact that any line passing through the origin is of the form $y=mx$. Use the fact that the slope of a line bisecting the coordinate axis is either 1 or -1. Hence find the required relation.

Complete step-by-step solution -

We have $a{{x}^{2}}+2bxy+b{{y}^{2}}=0$
Dividing both sides by ${{x}^{2}}$, we get
$a+2b\left( \dfrac{y}{x} \right)+b{{\left( \dfrac{y}{x} \right)}^{2}}=0$
We know that the equation of the line passing through origin is y = mx.
Hence we have $m=\dfrac{y}{x}$
Hence we get
$a+2bm+b{{m}^{2}}=0$
The above equation has either m = 1 or m = -1 as its root.
If m = 1, we have
$\begin{aligned} & a+2b+b=0 \\\ & \Rightarrow a+3b=0 \\\ \end{aligned}$
If m = -1, we have
$\begin{aligned} & a-2b+b=0 \\\ & \Rightarrow a=b \\\ \end{aligned}$
Hence options [b] and [c] are correct.

Note: When a = b, the equation becomes
$b{{x}^{2}}+2bxy+b{{y}^{2}}=0$
Dividing both sides by b, we get
${{x}^{2}}+2xy+{{y}^{2}}=0$
The graph of this pair is shown below

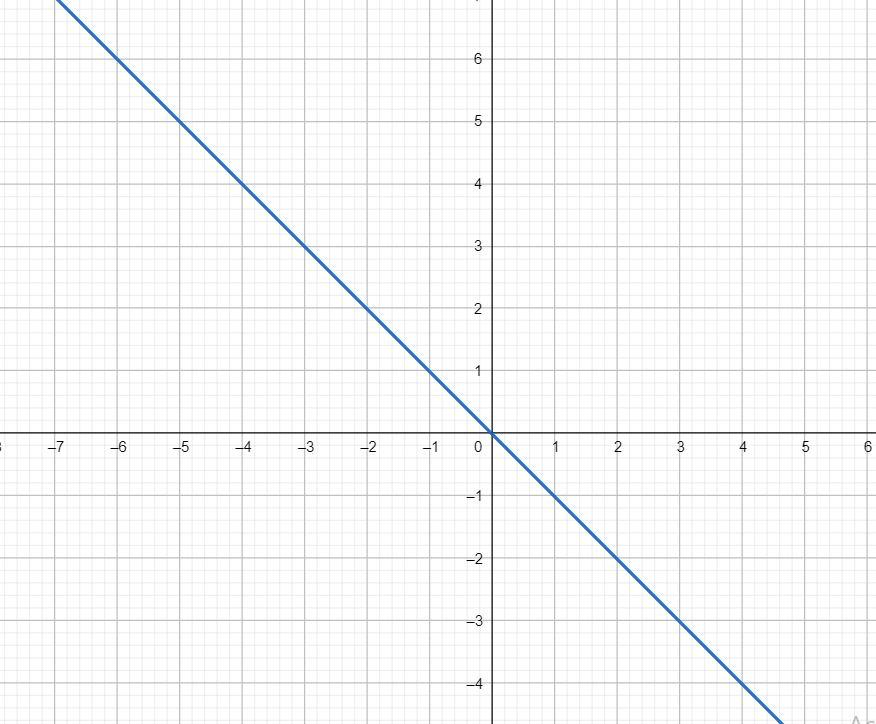
Which is a pair of coincident lines
Observe that the lines are bisecting the angle between x-axis and y-axis.
When a = -3b, the equation becomes
$-3b{{x}^{2}}+2bxy+b{{y}^{2}}=0$
Dividing both sides by b, we get
$-3{{x}^{2}}+2xy+{{y}^{2}}=0$
The graph of this pair is shown below

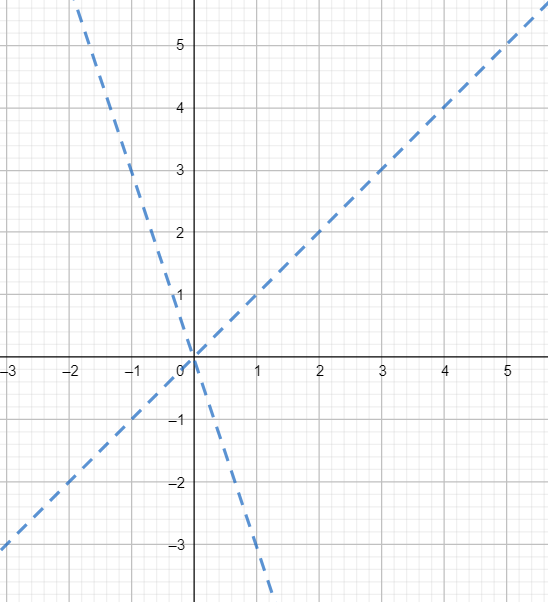
Observe that one line is bisecting the angle between x-axis and y-axis.