Solveeit Logo
Login

Question

Question: If one of the lines of \(m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0\) is a bisector of the...

If one of the lines of my2+(1−m2)xy−mx2=0m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0 is a bisector of the angle between the line xy=0xy=0, then find the value of m?
(a) -2
(b) 1
(c) 2
(d) −12\dfrac{-1}{2}

Explanation

Solution

We start solving the problem by finding the equation of lines present on the pairs of lines my2+(1−m2)xy−mx2=0m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0 and xy=0xy=0. We then find the angle between the lines present in xy=0xy=0 and find the slope of the line required to bisect the lines present in xy=0xy=0. We then equate this slope with the slopes of the lines present in my2+(1−m2)xy−mx2=0m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0 to get the required values of m.

Complete step-by-step solution
According to the problem, we are given that one of the lines of my2+(1−m2)xy−mx2=0m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0 is a bisector of the angle between the line xy=0xy=0.
Let us first find the lines present in the pair of lines my2+(1−m2)xy−mx2=0m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0.
So, we get my2+xy−m2xy−mx2=0m{{y}^{2}}+xy-{{m}^{2}}xy-m{{x}^{2}}=0.
⇒y(my+x)−mx(my+x)=0\Rightarrow y\left( my+x \right)-mx\left( my+x \right)=0.
⇒(y−mx)(my+x)=0\Rightarrow \left( y-mx \right)\left( my+x \right)=0.
⇒y−mx=0\Rightarrow y-mx=0 and my+x=0my+x=0.
⇒y=mx\Rightarrow y=mx and x=−myx=-my ---(1).
Now, let us find the lines present in the pair of lines xy=0xy=0.
So, we get x=0x=0 and y=0y=0. We know that this represents both axes and the angle between them is 90∘{{90}^{\circ }}. In order to bisect both axes we need the lines that make 45∘{{45}^{\circ }} with both x and y axes (assuming that the line bisects both axes in the first quadrant only).
So, the slope of the line should be tan⁡(45∘)=1\tan \left( {{45}^{\circ }} \right)=1.
Let us draw all the obtained information to get a better view.

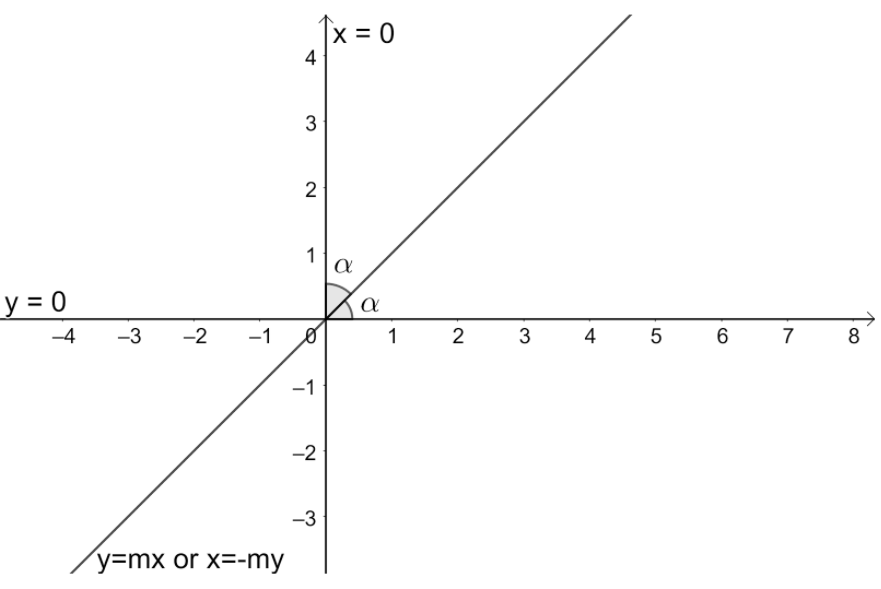
Let us assume that the line y=mxy=mx is the bisector of lines x=0x=0 and y=0y=0. We know that the slope of the y=mx+cy=mx+c is m. So, we get the value of m as 1 i.e., m=1m=1 ---(2).
Now, let us assume that the line x=−myx=-my is the bisector of lines x=0x=0 and y=0y=0.
So, we get y=−1mxy=\dfrac{-1}{m}x.
We know that the slope of the y=mx+cy=mx+c is m.
So, we get the −1m=1\dfrac{-1}{m}=1.
⇒m=−1\Rightarrow m=-1 ---(3).
From equations (2) and (3), we have found that the values for “m” are 1 and –1.
∴ The correct option for the given problem is (b).

Note: We should know that the line making 135∘{{135}^{\circ }} with x-axis will also bisect both x and y-axes but here we have taken an assumption that the angles lie in the first quadrant. Even if we take the slope of the line at the angle 135∘{{135}^{\circ }}, we get the same values for “m”. We should not make calculation mistakes while solving this problem. Similarly, we can expect problems to find the equation of the line that makes a triangle of area b which is formed when the line bisects both axes.