Solveeit Logo
Login

Question

Question: If one of the diameters of the circle given by the equation \[{x^2} + {y^2} - 4x + 6y - 12 = 0\], is...

If one of the diameters of the circle given by the equation x2+y2−4x+6y−12=0{x^2} + {y^2} - 4x + 6y - 12 = 0, is a chord of a circle ‘S’, whose center is a (−3, 2)\left( { - 3,\,2} \right), then the radius of ‘S’ is
A. 535\sqrt 3
B. 5
C. 10
D. 525\sqrt 2

Explanation

Solution

Circle: - The set of all points on a plane that are a fixed distance from a centre.
Chord: - A line that links two points on a circle is called a chord.


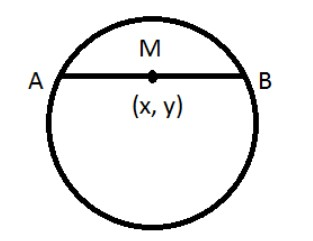
The equation of the chord of the circle x2+y2+2gx+2fy+c=0{x^2} + {y^2} + 2gx + 2fy + c = 0.
We will use this equation to solve the question.
With M(x1, y1)\left( {{x_1},\,{y_1}} \right)as the midpoint of the chord.
Centre −-g= −x2 = \,\dfrac{{ - x}}{2} or −f=−y2 - f = \dfrac{{ - y}}{2}
(−g, −f)=(−x2, −y2)\left( { - g,\, - f} \right) = \left( {\dfrac{{ - x}}{2},\,\dfrac{{ - y}}{2}} \right)
Radius ′r′=g2+g2−c'r' = \sqrt {{g^2} + {g^2} - c}
distan⁡ce=(x1−x2)2+(y2−y1)2dis\tan ce = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}
When two points (x1, y1)\left( {{x_1},\,{y_1}} \right)&(x2, y2)\left( {{x_2},\,{y_2}} \right) are given.

Complete step by step solution:

The equation of given circle
x2+y2−4x+6y−12=0{x^2} + {y^2} - 4x + 6y - 12 = 0.
Now we compare this equation with general equation i.e.
x2+y2+2gx+2fy+c=0{x^2} + {y^2} + 2gx + 2fy + c = 0.
Center, −g=−x2=−(42)=2 - g = \dfrac{{ - x}}{2} = - \left( {\dfrac{4}{2}} \right) = 2
−f=−y2=−(62)=−3- f = \dfrac{{ - y}}{2} = - \left( {\dfrac{6}{2}} \right) = - 3.
Centre (−g, −f)=(2, −3)\left( { - g,\, - f} \right) = \left( {2,\, - 3} \right)
r=g2+f2−cr = \sqrt {{g^2} + {f^2} - c}
=(2)2+(−3)2−(−12)= \sqrt {{{\left( 2 \right)}^2} + {{\left( { - 3} \right)}^2} - \left( { - 12} \right)}
=4+9+12= \sqrt {4 + 9 + 12}
=25=5= \sqrt {25} = 5
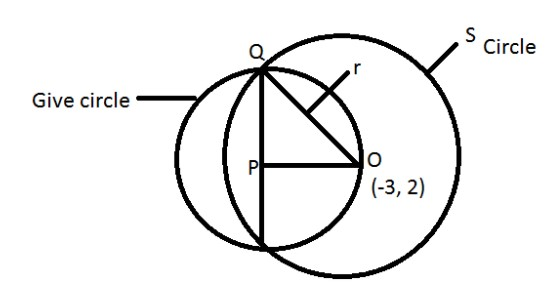
P is middle point of AB
P =(2, −3) = (2,\, - 3)
PQ =5 = 5.
The coordinate of ‘o’ is (−3, 2)( - 3,\,2)
In △POQ\vartriangle POQ:-
(PO)2+(PQ)2=r2{(PO)^2} + {(PQ)^2} = {r^2} [By Pythagoras theorem].
((x1−x2)2+(y1−y2)2)2+(PQ)2=r2{\left( {\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} } \right)^2} + {\left( {PQ} \right)^2} = {r^2}
((2+3)2+(−2−3)2)2+(PQ)2=r2{\left( {\sqrt {{{\left( {2 + 3} \right)}^2} + {{\left( { - 2 - 3} \right)}^2}} } \right)^2} + {\left( {PQ} \right)^2} = {r^2}
((5)2+(−5)2)2+(5)2=r2{\left( {\sqrt {{{\left( 5 \right)}^2} + {{\left( { - 5} \right)}^2}} } \right)^2} + {\left( 5 \right)^2} = {r^2}
(50)2+25=r2{\left( {\sqrt {50} } \right)^2} + 25 = {r^2}
50+25=r250 + 25 = {r^2}
75=r275 = {r^2}
r=35r = \sqrt[5]{3}

Hence, the radius of ‘S’ is 35\sqrt[5]{3}.

Note: In case, you are given the radius and the distance of the centre of circle to the chord you can apply this formula:
Chord length =2r2−d2= 2\sqrt {{r^2} - {d^2}}
Where, ‘r’ is the radius or the circle and ‘d’ is the perpendicular distance of the centre of the circle to the chord.