Question

If one face of a prism angle $30{} ^\circ$ and $\mu =\sqrt {2}$ is silvered, the incident ray retraces its initial path. The angle of incidence is:
(A) $60{} ^\circ$
(B)$30{} ^\circ$
(C)$45{} ^\circ$
(D)$90{} ^\circ$

Answer 1

In this question of ray optics, we are going to draw a diagram according to the question then, we are going to find the value of angle of refraction. Now, using Snell’s law we can write $\mu$ equals the ratio of sine of angle of incidence and angle of refraction. And finally, by putting the given data we can get the value of angle of incidence (i).

Complete step-by-step answer:
We already know that the incident light must fall normally on the silvered surface to retrace its initial path.
So, the as given in the question and the figure shown below,
Prism angle (P) =$30{} ^\circ$ and, $\mu =\sqrt {2}$,

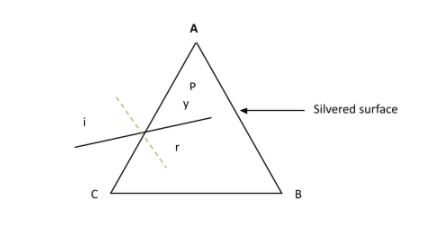
Now, we can write the equation of y as,
$y=90{} ^\circ -P=60{} ^\circ$and, we know from the theory of Ray optics that –
$y+r=90{} ^\circ$
$\Rightarrow \angle r=30{} ^\circ$ where, $\angle r$= angle of refraction.
We also know that the angle of incidence is denoted by i.
Snell’s law: According to this law of ray optics, when a ray passes between two media then, the ratio of the sine of angle of incidence and angle of refraction of that ray is constant.
$\mu =\dfrac {\sin \,i}{\sin \,r}$
So, applying Snell’s law, we get –
$\sin \,i=\sin \,r\,\times \,\mu$
$\Rightarrow \sin \,i=\sin \,30{}^\circ \,\times \,\sqrt{2}$
$\Rightarrow i= {{\sin} ^ {-1}}\left (\dfrac{\sqrt{2}}{2} \right)$
$\Rightarrow i= {{\sin} ^ {-1}}\left ( \dfrac{1}{\sqrt{2}} \right)$
$\Rightarrow \therefore I=45{} ^\circ$

So, the correct answer is “Option C”.

Note: Snell’s law is one of the most important laws of ray optics. Prism angle (P): It is defined as the angle that is formed at the surface of the prism when ray enters and leaves the prism. Whereas, Angle of deviation ($\mu$): it is defined as the angle which is a result of the difference between the angle of incidence and angle of refraction.