Solveeit Logo
Login

Question

Question: If one end of the minor axis forms an equilateral triangle with the foci of the ellipse, then find t...

If one end of the minor axis forms an equilateral triangle with the foci of the ellipse, then find the eccentricity of the ellipse.
A.12\dfrac{1}{2}
B.12\dfrac{1}{{\sqrt 2 }}
C.32\dfrac{{\sqrt 3 }}{2}
D.14\dfrac{1}{4}

Explanation

Solution

The major axis bisects the equilateral triangle in the middle and forms two right angled triangles. Take one right angled triangle and use Pythagoras theorem which states that , “In a right angled triangle, the square of the longest side (hypotenuse) is equal to the sum of the squares of the two other sides”
⇒\Rightarrow H2=P2+B2{H^2} = {P^2} + {B^2} Where H is hypotenuse, P is the perpendicular and B is the base, to find the side joining foci to one point of triangle formed on the minor axes. Then find the value of a and b and use the formula of eccentricity of ellipse which is given by-
Eccentricity of ellipse=1−b2a2\sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}} where a and b are half lengths of major and minor axes respectively.

Complete step-by-step answer:
Let BB’ be the end of the minor axis forming an equilateral triangleΔABB′\Delta ABB' with foci A of the ellipse. Now we know that the length of major axes of ellipse is 2a2a and length of minor axes is 2b2b. Then, let O be the centre where the major axis and minor axes meet. So we get,
OA=a, OB=OB’=b as BB’=2b2b

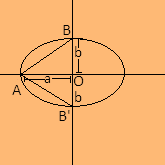
Now since it is clear from the diagram ΔAOB′\Delta AOB' is a right angled triangle where OA=’a’ and OB’=b.
We have to find AB’.
By Pythagoras theorem,
In a right angled triangle, the square of the longest side (hypotenuse) is equal to the sum of the squares of the two other sides. It is written as-
H2=P2+B2{H^2} = {P^2} + {B^2}
Where H is hypotenuse, P is the perpendicular and B is the base.
Here AB’ is the hypotenuse, OB’ is the base and OA is the perpendicular. Then on putting the values in the formula we get,
⇒\Rightarrow AB′2=OB′2+OA2AB{'^2} = OB{'^2} + O{A^2}
On putting OA=’a’ and OB’=b, we get-
⇒AB′2=b2+a2\Rightarrow AB{'^2} = {b^2} + {a^2}
⇒AB′=b2+a2\Rightarrow AB' = \sqrt {{b^2} + {a^2}}
Now we know that ΔABB′\Delta ABB' is an equilateral triangle then, all the sides of given triangle are equal.
⇒\Rightarrow AB’=BB’
On putting the values we get,
⇒b2+a2=2b\Rightarrow \sqrt {{b^2} + {a^2}} = 2b
On squaring both side we get,
⇒b2+a2=4b2\Rightarrow {b^2} + {a^2} = 4{b^2}
On simplifying we get,
⇒a2=4b2−b2\Rightarrow {a^2} = 4{b^2} - {b^2}
⇒a2=3b2\Rightarrow {a^2} = 3{b^2}
On taking the ratio ofb2a2\dfrac{{{b^2}}}{{{a^2}}} , we get-
⇒b2a2=13\Rightarrow \dfrac{{{b^2}}}{{{a^2}}} = \dfrac{1}{3}
Now we know that eccentricity of ellipse=1−b2a2\sqrt {1 - \dfrac{{{b^2}}}{{{a^2}}}}
On putting the values we get,
Eccentricity of ellipse=1−13=3−13\sqrt {1 - \dfrac{1}{3}} = \sqrt {\dfrac{{3 - 1}}{3}}
On solving we get,
Eccentricity of ellipse=23\sqrt {\dfrac{2}{3}}

Note: Here, we have to find the values of ‘a’ and b to calculate the eccentricity of ellipse which is not easy to find. Hence we find the ratio of b/a by using the value of the sides of the equilateral triangle. Equilateral triangle is a triangle which has equal sides and equal angles which means AB= AB’=BB’. So the students can also take triangle AOB to use Pythagoras theorem and find the value of side AB.
On putting the values in the theorem-
⇒\Rightarrow AB2=OB2+OA2A{B^2} = O{B^2} + O{A^2}
⇒AB2=b2+a2\Rightarrow A{B^2} = {b^2} + {a^2}
⇒AB=b2+a2\Rightarrow AB = \sqrt {{b^2} + {a^2}}