Question

If on a given base, a triangle be described such that the sum of the tangents of the base angles is constant, then the locus of the vertex is:
A. a circle
B. a parabola
C. an ellipse
D. a hyperbola

Answer 1

First we need to draw a triangle on the coordinate plane. We draw a triangle by assuming $BC$ as the base of the triangle and the length of $BC=2a$. Then, we draw a perpendicular to base at point $D$. Then, we use the property of tangent in the form of trigonometric ratio, which is given by
$\tan \theta =\dfrac{\text{Perpendicular}}{\text{base}}$
Then, by adding the tangents of the base angles and solving these further we get the desired answer.

Complete step by step answer:
We have been given that a triangle be described such that the sum of the tangents of the base angles is constant.
Let us draw a diagram on the coordinate plane by assuming that the given base of the triangle is $BC$ and the length of $BC=2a$

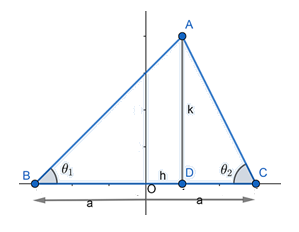
Let the coordinates of $B\left( -a,0 \right)$ and $C\left( a,0 \right)$. Also, let the coordinates of $A\left( h,k \right)$.
We draw a perpendicular from $A$ to base $BC$, which meets $BC$ at point $D$.
So, we have $OB=OC=a,OD=h,AD=k$ .
Now, we have given that the sum of the tangents of the base angles is constant.
So, we have $\tan {{\theta }_{1}}+\tan {{\theta }_{2}}=c.....(i)$ where, $c=\text{constant}$
Now, let us consider $\Delta ABD$,
Now we know that $\tan \theta =\dfrac{\text{Perpendicular}}{\text{base}}$
So, we have $\tan {{\theta }_{1}}=\dfrac{AD}{BD}$
Now, substituting values, we get
$\begin{aligned} & \Rightarrow \tan {{\theta }_{1}}=\dfrac{k}{OB+OD} \\\ & \Rightarrow \tan {{\theta }_{1}}=\dfrac{k}{a+h} \\\ \end{aligned}$
Now, let us consider $\Delta ADC$,
Now we know that $\tan \theta =\dfrac{\text{Perpendicular}}{\text{base}}$
So, we have $\tan {{\theta }_{2}}=\dfrac{AD}{DC}$
Now, substituting values, we get
$\begin{aligned} & \Rightarrow \tan {{\theta }_{2}}=\dfrac{k}{OC-OD} \\\ & \Rightarrow \tan {{\theta }_{2}}=\dfrac{k}{a-h} \\\ \end{aligned}$
Now, substituting the values in equation (i), we get
$\begin{aligned} & \tan {{\theta }_{1}}+\tan {{\theta }_{2}}=c \\\ & \Rightarrow \dfrac{k}{a+h}+\dfrac{k}{a-h}=c \\\ \end{aligned}$
Now, solving further we have
$\Rightarrow \dfrac{k\left( a-h \right)+k\left( a+h \right)}{\left( a+h \right)\left( a-h \right)}=c$
Now, we know that $\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}$
So, we have
$\begin{aligned} & \dfrac{k\left( a-h \right)+k\left( a+h \right)}{{{a}^{2}}-{{h}^{2}}}=c \\\ & \Rightarrow ak-kh+ak+kh=c\left( {{a}^{2}}-{{h}^{2}} \right) \\\ & \Rightarrow 2ak=c\left( {{a}^{2}}-{{h}^{2}} \right) \\\ \end{aligned}$
Therefore we can write
$\begin{aligned} & \Rightarrow 2ak=c{{a}^{2}}-c{{h}^{2}} \\\ & \Rightarrow c{{h}^{2}}=c{{a}^{2}}-2ak \\\ & \Rightarrow {{h}^{2}}=\dfrac{c{{a}^{2}}}{c}-\dfrac{2ak}{c} \\\ & \Rightarrow {{h}^{2}}=\dfrac{-2a}{c}\left( k-\dfrac{ca}{2} \right) \\\ \end{aligned}$
Now, if we replace $h$ by $x$ and $k$ by $y$, we get
$\Rightarrow {{x}^{2}}=\dfrac{-2a}{c}\left( y-\dfrac{ca}{2} \right)$
Now, we know that the equation of parabola is given by
$\begin{aligned} & \Rightarrow y-k=a{{\left( x-h \right)}^{2}} \\\ & \Rightarrow x-h\text{=}a{{\left( y-k \right)}^{2}} \\\ \end{aligned}$
So, the equation we get is comparable to parabola.
So, the locus of the vertex is parabola.
Option B is the correct answer.

Note:
When we draw a diagram we can take vertex $A,B,C$ anywhere. The equations of circle, hyperbola and ellipse are as follows:
$\begin{aligned} & \text{Circle }{{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}} \\\ & \text{Ellipse }\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}+\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 \\\ & \text{Hyperbola }\dfrac{{{\left( x-h \right)}^{2}}}{{{a}^{2}}}-\dfrac{{{\left( y-k \right)}^{2}}}{{{b}^{2}}}=1 \\\ \end{aligned}$