Question

If $\omega$ is a cube root of unity and $\omega \neq 1$, then $\left|2\cos\left(\sum_{k=1}^{10}(k-\omega)(k-\omega^2)\frac{\pi}{1350}\right)\right|$ is equal to

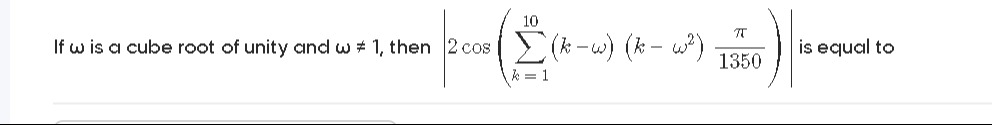
• A. 0
• B. 1
• C. 2
• D. 3

Answer 1

Answer: (B)

1

Answer 2

Given $\omega$ is a cube root of unity with $\omega \neq 1$, we have:

$$\omega + \omega^2 = -1 \quad \text{and} \quad \omega\omega^2 = 1.$$

Thus,

$$(k-\omega)(k-\omega^2)= k^2 - k(\omega+\omega^2) + \omega\omega^2 = k^2+k+1.$$

Summing from $k=1$ to $10$:

$$\sum_{k=1}^{10}(k^2+k+1)=\sum_{k=1}^{10}k^2+\sum_{k=1}^{10}k+10 = 385+55+10 = 450.$$

The angle becomes:

$$450\cdot\frac{\pi}{1350}=\frac{\pi}{3}.$$

So,

$$2\cos\left(\frac{\pi}{3}\right)=2\left(\frac{1}{2}\right)=1.$$

Taking the absolute value, we get $\left| 1 \right|=1$.