Question

If OB is the semi-minor axis of an ellipse, ${F_1}$ and ${F_2}$ are its foci and the angle between ${F_1}B$ and
${F_2}B$ is a right angle, then the square of the eccentricity of the ellipse is
A) $\dfrac{1}{2}$
B) $\dfrac{1}{{\sqrt 2 }}$
C) $\dfrac{1}{{2\sqrt 2 }}$
D) $\dfrac{1}{4}$

Answer 1

Here first we will find the slopes of ${F_1}B$ and ${F_2}B$ using their respective coordinates and then we will use the concept of slopes of perpendicular lines and the formula of eccentricity to get the desired answer.

If two lines are perpendicular then the product of their slopes is equal to -1.
The eccentricity for an ellipse with equation $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is given by:-
${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$……………………………..(1)

Complete step-by-step answer:

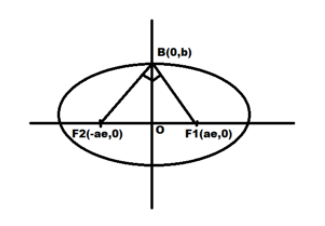
Since it is given that ${F_1}$ and ${F_2}$ are foci of ellipse
Hence the coordinates of ${F_1}$ and ${F_2}$ are ${F_1} \equiv \left( {ae,0} \right)$ and ${F_2} \equiv \left( { - ae,0} \right)$
Also OB is the minor axis therefore the coordinate of B is $B \equiv \left( {0,b} \right)$
Now we will find the slope of line ${F_1}B$.

The slope m of a line passing through two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by:-

$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

Hence the slope ${m_1}$ of ${F_1}B$ having endpoints ${F_1} \equiv \left( {ae,0} \right)$and $B \equiv \left( {0,b} \right)$ is given by:-
${m_1} = \dfrac{{b - 0}}{{0 - ae}}$

Solving it further we get:-
${m_1} = \dfrac{{ - b}}{{ae}}$…………………………(2)

Now we will find the slope of line ${F_2}B$.

The slope m of a line passing through two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given by:-

$m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$

Hence the slope ${m_2}$ of ${F_2}B$ having endpoints ${F_2} \equiv \left( { - ae,0} \right)$and $B \equiv \left( {0,b} \right)$ is given by:-
${m_2} = \dfrac{{b - 0}}{{0 - \left( { - ae} \right)}}$

Solving it further we get:-

${m_2} = \dfrac{b}{{ae}}$……………………………………..(3)

Now we know that if two lines are perpendicular then the product of their slopes is equal to -1.
Now we are given that the angle between ${F_1}B$ and ${F_2}B$ is a right angle
Therefore ${F_1}B$ and ${F_2}B$ are perpendicular to each other therefore the product of their slopes will be -1.

Hence multiplying equation 2 and equation 3 we get:-

${m_1} \times {m_2} = - 1$
Putting in the values from equation 2 and 3 we get:-

$\dfrac{{ - b}}{{ae}} \times \dfrac{b}{{ae}} = - 1$

Solving it further we get:-

$$\dfrac{{ - {b^2}}}{{{a^2}{e^2}}} = - 1 \\\ \dfrac{{{b^2}}}{{{a^2}}} = {e^2}...........................\left( 4 \right) \\\$$

Now from equation 1 we get:-

$${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}} \\\ \Rightarrow \dfrac{{{b^2}}}{{{a^2}}} = 1 - {e^2} \\\$$

Putting this value in equation 4 we get:-

$1 - {e^2} = {e^2}$

Solving it further we get:-

$$2{e^2} = 1 \\\ \Rightarrow {e^2} = \dfrac{1}{2} \\\$$

So, the correct answer is “Option A”.

Note: Students should use the correct formula for eccentricity of the ellipse.
The eccentricity for an ellipse with equation $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is given by:-
${e^2} = 1 - \dfrac{{{b^2}}}{{{a^2}}}$ for $a > b$
If $a < b$ then eccentricity is given by:-
${e^2} = 1 - \dfrac{{{a^2}}}{{{b^2}}}$