Question
Question: If no two books are alike, in how many ways 2 red, 3 green and 4 blue books are arranged on a shelf ...
If no two books are alike, in how many ways 2 red, 3 green and 4 blue books are arranged on a shelf so that all the books of the same colour are together?
Solution
Hint: Arrangement of ‘n’ things can be given by relation ‘n!’. Just analyse only one arrangement of books of the same colours placed together. Now try to arrange the books in groups of the same colour and hence find the arrangement of whole books by multiplying the arrangement of each color book.
“Complete step-by-step answer:”
As it is given that no two books are alike which means all (2 + 3 + 4) = 9 books are distinct to each other. So, we have 2 books of red colour, 3 of green and 4 of blue colour. Now, we need to determine the number of arrangements of the whole books on shelf such that all the books of the same colour are together. It means that 2 red books will take shelf together, 3 green books will tie in shelf together and similarly, all 4 books of blue colour will be together in the self.
Let us suppose the name of books of red, green and blue colour books are represented by letters R, G and B. Now, two books of red colour can be named as R1 and R2 .
3 green books can be named as G1,G2 and G3 .
4 blue books can be named as B1,B2,B3 and B4
Now, as per the given condition all books of the same colour are together. Hence, we can represent one combination of red, green and blue books in self as
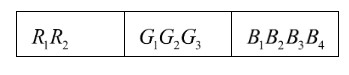
Now, we can observe that only red books can be arranged in themselves not with others, similarly green books can be arranged within themselves not with any other colour and hence similar for blue books as well.
Hence, same colour books can be arranged within themselves only not with any other colour.
So, we can get linear arrangements of n things as ‘n!’.
Hence, arrangement of red books = 2!
Arrangement of green books = 3!
Arrangement of blue books = 4!
Now, we can get an arrangement of all books such that books of the same colour will lie together and can be given by multiplying the arrangements of each colour book as given above.
Hence, arrangement of books as per the given condition
=2!×3!×4!=2×6×24=12×24=288
Therefore, we can arrange the books by 288 ways so that all the books of the same colour are together.
Note: A very simple mistake can happen here by the students that one arranges the whole books by 9!, without using the condition that all books of the same colour will lie together.
Another approach of going wrong would be that one may try to add the arrangements of each colour book (2! + 3! + 4!), which is wrong, because we need to find the arrangements of whole books. So, take care of it as well, students do get confused with fundamental laws of permutations and combinations i.e. where we need to pass the selections or permutations or multiply the selections or permutations. So, be clear with basic rules for these kinds of questions.
