Question
Question: If n ∈ N and $(1 + x + x^2)^n = \sum_{r=0}^{2n} a_r x^r$, then $\sum_{r=0}^{n} (-1)^r a_r {}^nC_r$ i...
If n ∈ N and (1+x+x2)n=∑r=02narxr, then ∑r=0n(−1)rarnCr is equal to
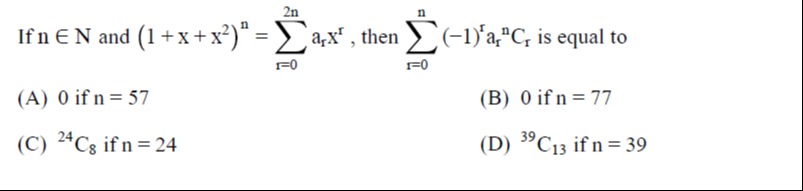
0 if n = 57
0 if n = 77
24C8 if n = 24
39C13 if n = 39
(B), (C), (D)
Solution
Let the given equation be (1+x+x2)n=∑r=02narxr. We are asked to find the value of the sum S=∑r=0n(−1)rarnCr.
Consider the product of the series expansion of (1+x+x2)n and the series expansion of (1−1/x)n. (1+x+x2)n=∑r=02narxr. (1−1/x)n=∑k=0nnCk(−1/x)k=∑k=0n(−1)knCkx−k.
The product is (1+x+x2)n(1−1/x)n=(∑r=02narxr)(∑k=0n(−1)knCkx−k). The coefficient of x0 (the constant term) in this product is obtained by summing the products of terms arxr and (−1)knCkx−k such that r−k=0, i.e., r=k. The coefficient of x0 is ∑r=0min(2n,n)ar(−1)rnCr. Since the upper limit of the sum we want to evaluate is n, and nCr=0 for r>n, we can write the constant term as ∑r=02nar(−1)rnCr. As nCr=0 for r>n, this sum is equal to ∑r=0nar(−1)rnCr=∑r=0n(−1)rarnCr=S.
Now let's evaluate the product (1+x+x2)n(1−1/x)n in a different way. (1+x+x2)n(1−1/x)n=(1+x+x2)n(xx−1)n=xn(1+x+x2)n(x−1)n. Using the identity (x−1)(x2+x+1)=x3−1, we have (x−1)(1+x+x2)=x3−1. So, the expression becomes xn((1+x+x2)(x−1))n=xn(x3−1)n.
Now, expand (x3−1)n using the binomial theorem: (x3−1)n=∑k=0nnCk(x3)k(−1)n−k=∑k=0n(−1)n−knCkx3k.
So, xn(x3−1)n=xn∑k=0n(−1)n−knCkx3k=∑k=0n(−1)n−knCkx3k−n.
The constant term in this expansion is obtained when the exponent of x is 0, i.e., 3k−n=0, or 3k=n. For the constant term to exist, n must be a multiple of 3. If n is a multiple of 3, let n=3m for some integer m. Then 3k=3m, which gives k=m. Since 0≤k≤n, we must have 0≤m≤3m, which is true for m≥0. The value of k is n/3. The constant term is (−1)n−n/3nCn/3. If n=3m, the constant term is (−1)3m−mnCm=(−1)2mnCm=((−1)2)mnCm=1mnCm=nCm. Since m=n/3, the constant term is nCn/3.
If n is not a multiple of 3, there is no integer k in the range 0≤k≤n such that 3k=n. In this case, the coefficient of x0 is 0.
So, the sum S=∑r=0n(−1)rarnCr is equal to:
-
nCn/3 if n≡0(mod3).
-
0 if n≡0(mod3).
Now let's check the given options:
(A) 0 if n=57. 57=3×19. n≡0(mod3). The sum is 57C19. So this option is incorrect.
(B) 0 if n=77. 77=3×25+2. n≡0(mod3). The sum is 0. So this option is correct.
(C) 24C8 if n=24. 24=3×8. n≡0(mod3). The sum is 24C24/3=24C8. So this option is correct.
(D) 39C13 if n=39. 39=3×13. n≡0(mod3). The sum is 39C39/3=39C13. So this option is correct.
Since the question asks which of the options is equal to the sum, and multiple options are correct, this is a multiple correct options question.
