Question

If n > 0 and exactly 15 integers satisfy $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$, then sum of digits of the least possible value of n is

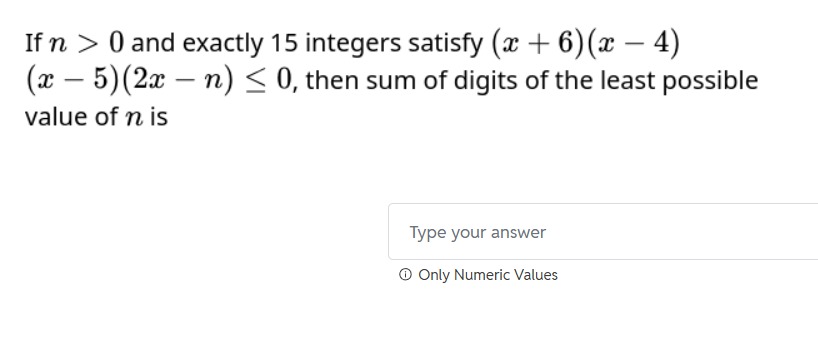
• A. The inequality $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$ has roots $-6, 4, 5, n/2$. Since $n>0$, $n/2>0$. Analyzing the sign of the polynomial $P(x)$ in intervals defined by these roots, and considering the condition that exactly 15 integers satisfy the inequality, we found that the roots must be ordered as $-6, 4, 5, n/2$. This leads to the solution set $[-6, 4] \cup [5, n/2]$. Counting the integers in this set, we get $11 + (\lfloor n/2 \rfloor - 5 + 1) = \lfloor n/2 \rfloor + 7$. Setting this equal to 15, we get $\lfloor n/2 \rfloor = 8$, which implies $8 \le n/2 < 9$, or $16 \le n < 18$. The least possible integer value for $n$ is 16. The sum of digits of 16 is $1+6=7$.
• B. The inequality $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$ has roots $-6, 4, 5, n/2$. Since $n>0$, $n/2>0$. Analyzing the sign of the polynomial $P(x)$ in intervals defined by these roots, and considering the condition that exactly 15 integers satisfy the inequality, we found that the roots must be ordered as $-6, n/2, 4, 5$. This leads to the solution set $[-6, n/2] \cup [4, 5]$. Counting the integers in this set, we get $(\lfloor n/2 \rfloor + 7) + 2 = \lfloor n/2 \rfloor + 9$. Setting this equal to 15, we get $\lfloor n/2 \rfloor = 6$, which implies $6 \le n/2 < 7$, or $12 \le n < 14$. This contradicts the condition $0 < n/2 < 4$.
• C. The inequality $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$ has roots $-6, 4, 5, n/2$. Since $n>0$, $n/2>0$. Analyzing the sign of the polynomial $P(x)$ in intervals defined by these roots, and considering the condition that exactly 15 integers satisfy the inequality, we found that the roots must be ordered as $-6, 4, n/2, 5$. This leads to the solution set $[-6, 4] \cup [n/2, 5]$. Counting the integers in this set, we get $11 + (5 - \lceil n/2 \rceil + 1) = 17 - \lceil n/2 \rceil$. Setting this equal to 15, we get $\lceil n/2 \rceil = 2$, which implies $1 < n/2 \le 2$, or $2 < n \le 4$. This contradicts the condition $4 < n/2 < 5$.
• D. The least possible value of n is 17. The sum of digits of 17 is $1+7=8$.

Answer 1

Answer: (A)

The inequality $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$ has roots $-6, 4, 5, n/2$. Since $n>0$, $n/2>0$. Analyzing the sign of the polynomial $P(x)$ in intervals defined by these roots, and considering the condition that exactly 15 integers satisfy the inequality, we found that the roots must be ordered as $-6, 4, 5, n/2$. This leads to the solution set $[-6, 4] \cup [5, n/2]$. Counting the integers in this set, we get $11 + (\lfloor n/2 \rfloor - 5 + 1) = \lfloor n/2 \rfloor + 7$. Setting this equal to 15, we get $\lfloor n/2 \rfloor = 8$, which implies $8 \le n/2 < 9$, or $16 \le n < 18$. The least possible integer value for $n$ is 16. The sum of digits of 16 is $1+6=7$.

Answer 2

The given inequality is $(x + 6)(x - 4)(x - 5)(2x - n) \le 0$, where $n > 0$. Let $P(x) = (x + 6)(x - 4)(x - 5)(2x - n)$. The roots of the polynomial $P(x)$ are $x = -6$, $x = 4$, $x = 5$, and $x = n/2$. Since $n > 0$, we have $n/2 > 0$. The fixed roots are $-6, 4, 5$. The root $n/2$ is positive and can be located relative to $4$ and $5$.

The leading coefficient of $P(x)$ is $1 \times 1 \times 1 \times 2 = 2$, which is positive. Thus, $P(x) \to \infty$ as $x \to \infty$ and $P(x) \to \infty$ as $x \to -\infty$. The regions where $P(x) \le 0$ will be between the roots.

We consider the possible orderings of the roots:

Case 1: $0 < n/2 < 4$ (i.e., $0 < n < 8$) The ordered roots are $-6, n/2, 4, 5$. $P(x) \le 0$ for $x \in [-6, n/2] \cup [4, 5]$. The integers in $[4, 5]$ are $4, 5$ (2 integers). The integers in $[-6, n/2]$ are $-6, -5, \dots, \lfloor n/2 \rfloor$. The number of integers is $\lfloor n/2 \rfloor - (-6) + 1 = \lfloor n/2 \rfloor + 7$. The total number of integers satisfying the inequality is $(\lfloor n/2 \rfloor + 7) + 2 = \lfloor n/2 \rfloor + 9$. We are given that this number is 15: $\lfloor n/2 \rfloor + 9 = 15 \implies \lfloor n/2 \rfloor = 6$. This implies $6 \le n/2 < 7$, so $12 \le n < 14$. This contradicts our assumption for this case ($0 < n < 8$). So, there is no solution in this case.

Case 2: $4 < n/2 < 5$ (i.e., $8 < n < 10$) The ordered roots are $-6, 4, n/2, 5$. $P(x) \le 0$ for $x \in [-6, 4] \cup [n/2, 5]$. The integers in $[-6, 4]$ are $-6, -5, \dots, 4$. The number of integers is $4 - (-6) + 1 = 11$. The integers in $[n/2, 5]$ are $\lceil n/2 \rceil, \dots, 5$. The number of integers is $5 - \lceil n/2 \rceil + 1 = 6 - \lceil n/2 \rceil$. The total number of integers is $11 + (6 - \lceil n/2 \rceil) = 17 - \lceil n/2 \rceil$. We need $17 - \lceil n/2 \rceil = 15 \implies \lceil n/2 \rceil = 2$. This implies $1 < n/2 \le 2$, so $2 < n \le 4$. This contradicts our assumption for this case ($8 < n < 10$). So, there is no solution in this case.

Case 3: $n/2 > 5$ (i.e., $n > 10$) The ordered roots are $-6, 4, 5, n/2$. $P(x) \le 0$ for $x \in [-6, 4] \cup [5, n/2]$. The integers in $[-6, 4]$ are $-6, -5, \dots, 4$. The number of integers is $4 - (-6) + 1 = 11$. The integers in $[5, n/2]$ are $5, 6, \dots, \lfloor n/2 \rfloor$. The number of integers is $\lfloor n/2 \rfloor - 5 + 1 = \lfloor n/2 \rfloor - 4$. The total number of integers is $11 + (\lfloor n/2 \rfloor - 4) = \lfloor n/2 \rfloor + 7$. We need $\lfloor n/2 \rfloor + 7 = 15 \implies \lfloor n/2 \rfloor = 8$. This implies $8 \le n/2 < 9$, so $16 \le n < 18$. This is consistent with our assumption for this case ($n > 10$).

The possible integer values for $n$ in this range are $16$ and $17$. We are looking for the least possible value of $n$. The least integer value is $n = 16$.

We must also check the boundary cases where $n/2$ coincides with $4$ or $5$. If $n/2 = 4$ (i.e., $n=8$), the roots are $-6, 4, 4, 5$. The inequality becomes $(x+6)(x-4)^2(x-5) \le 0$. Since $(x-4)^2 \ge 0$, this is equivalent to $(x+6)(x-5) \le 0$, which holds for $-6 \le x \le 5$. The integers are $-6, \dots, 5$, totaling $5 - (-6) + 1 = 12$ integers, not 15. If $n/2 = 5$ (i.e., $n=10$), the roots are $-6, 4, 5, 5$. The inequality becomes $(x+6)(x-4)(x-5)^2 \le 0$. Since $(x-5)^2 \ge 0$, this is equivalent to $(x+6)(x-4) \le 0$, which holds for $-6 \le x \le 4$. The integers are $-6, \dots, 4$, totaling $4 - (-6) + 1 = 11$ integers, not 15.

Therefore, the least possible integer value of $n$ is 16. The question asks for the sum of the digits of the least possible value of $n$. For $n=16$, the sum of digits is $1 + 6 = 7$.

The final answer is $\boxed{7}$.