Question

If modulus and amplitude of a complex number are 2 and $\dfrac{2\pi }{3}$ respectively, then the number is:
(A). $1i\sqrt{3}$
(B). $1+i\sqrt{3}$
(C). $-1+i\sqrt{3}$
(D). $-1i\sqrt{3}$

Answer 1

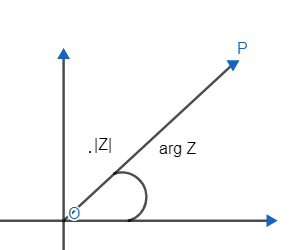
Hint: We will be using the concepts of complex numbers to solve the problem. We will be using a modulus and arrangement way of representing a complex number. We know that the modulus of a complex number Z=x+iy is $\left| Z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$ and argument of a complex number is the angle between positive real axis in complex plane and vector OP.

Complete step-by-step solution -
Now, we have been given the modulus and amplitude of a complex number as 2 and $\dfrac{2\pi }{3}$ respectively and we have to find the complex number.
Now, we know that a complex number can be represented as

$Z=\left| Z \right|$ (Cos arg z + i Sin (arg z))…………….. (1)
Where $\left| Z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$ is the modulus of the complex number.
$\arg ={{\tan }^{-1}}\left( \dfrac{y}{x} \right)$ and arg z lies between $-\pi$ to $\pi$ also in diagram we can see that arg z is the angle between positive real axis and vector OP.
Now, we have been given that the modulus of complex number is 2 and the arg z is $\dfrac{2\pi }{3}$. Therefore, from (1) the complex number is $Z=2\left[ \cos \left( \dfrac{2\pi }{3} \right)+i\sin \left( \dfrac{2\pi }{3} \right) \right]$ .
$Z=2\left[ -\dfrac{1}{2}+\dfrac{i\sqrt{3}}{2} \right]$ .
$Z=-1+i\sqrt{3}$ .
Hence, the correct answer is option (c).

Note: To solve these types of questions it is important to draw a figure representing the complex number then use the appropriate formula. Like in this case modulus and argument from to represent the answer.