Question
Question: If maximum energy is stored in a capacitor at \(t=0\) then find the time after which current in the ...
If maximum energy is stored in a capacitor at t=0 then find the time after which current in the circuit will be maximum.
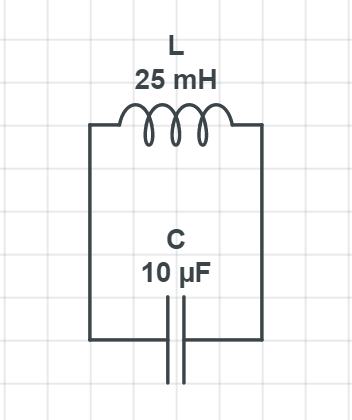
Solution
In a LCR circuit, the inductor L, capacitance C and resistance R are connected to a AC source. Here the LCR is connected in series circuit; it can also be connected in parallel circuit. Then the phase difference between the current and the voltage is θ generally.
Formula used:
T=2πLC
Complete step by step answer:
We know that the source of an AC circuit is sinusoidal. Then there is a phase difference between the voltage and current. If the phase difference between the current and voltage is zero, then both are said to be in phase, and if the phase difference is not equal to zero, then both are said to be out of phase. Resonance is a special condition, which is observed when RLC is connected in series; here there is no phase difference between the current and the voltage.
We know that the frequency of the circuit is given as,ω=LC1
⟹T=2πLC, where T is the time-period of one cycle.
Here, we have LC circuit, and given that, L=25mH and C=10μF, substituting the values, we get,
T=2π25×10−3×10×10−6
⟹T=2π25×10−8
⟹T=2π×5×10−4
∴T=π×10−3s
Since the AC is sinusoidal in nature and the time-period of the wave is T=π×10−3s, we know that at 4T, the capacitance discharges the charge stored in it, and thus the current is maximum. Hence at Tmax=4T=4π×10−3
∴Tmax=4πms
So, the correct answer is “Option B”.
Note:
Z is the impedance of the circuit or the total resistance offered by the circuit, it is given as Z=R2+(XL−XC)2. Here XL,XC are the inductive reactance and the capacitive reactance. Using the frequency of the circuit, we can solve this sum.
