Solveeit Logo
Login

Question

Question: If matrix $A = \begin{bmatrix} 1 & 2 \\ 4 & 3 \end{bmatrix}$ is such that $AX = I$, where I is 2 x 2...

If matrix A=[1243]A = \begin{bmatrix} 1 & 2 \\ 4 & 3 \end{bmatrix} is such that AX=IAX = I, where I is 2 x 2 unit matrix, then X=X =

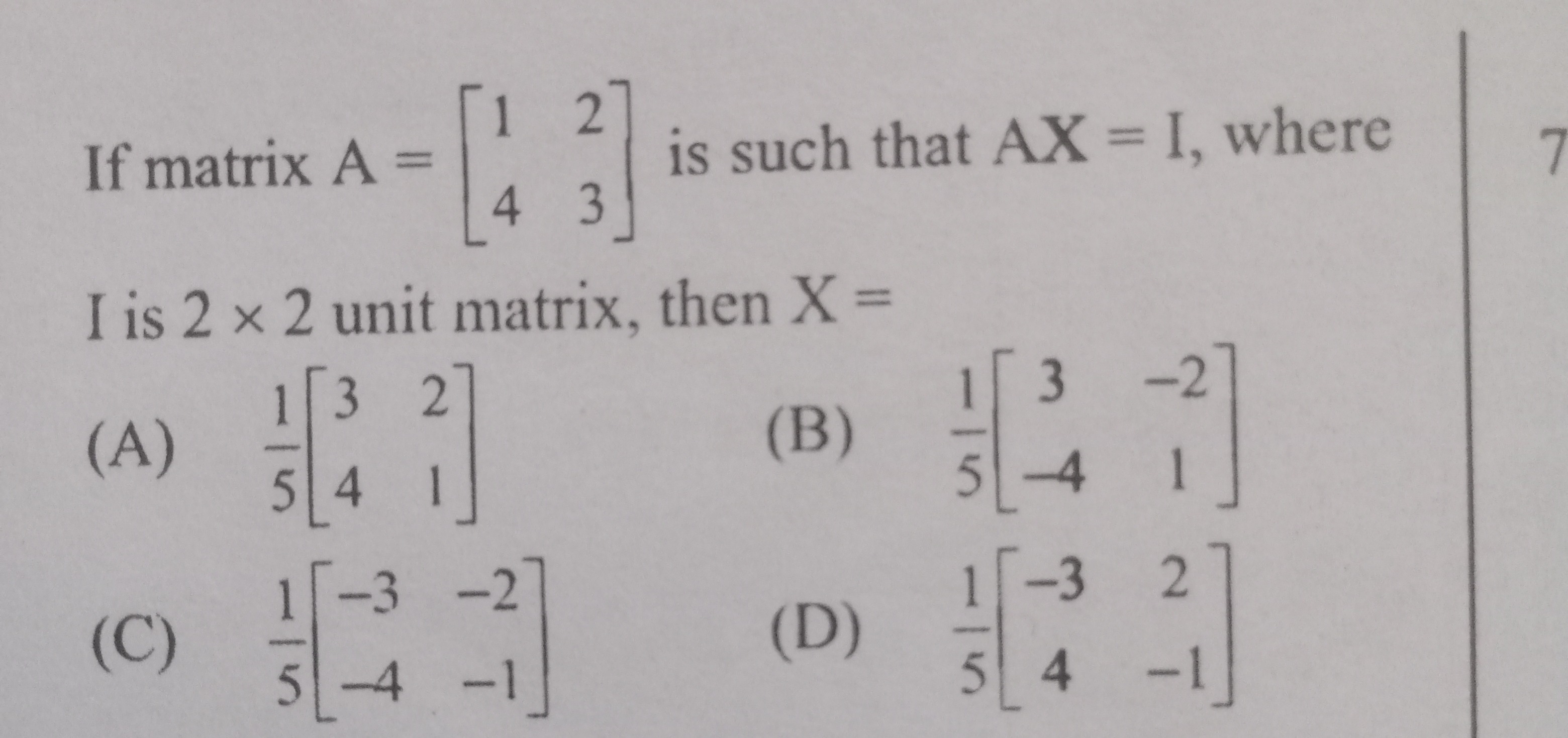
A

15[3241]\frac{1}{5}\begin{bmatrix} 3 & 2 \\ 4 & 1 \end{bmatrix}

B

15[3−2−41]\frac{1}{5}\begin{bmatrix} 3 & -2 \\ -4 & 1 \end{bmatrix}

C

15[−3−2−4−1]\frac{1}{5}\begin{bmatrix} -3 & -2 \\ -4 & -1 \end{bmatrix}

D

15[−324−1]\frac{1}{5}\begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}

Answer

15[−324−1]\frac{1}{5}\begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}

Explanation

Solution

Given AX=IAX = I, X=A−1X = A^{-1}.

A=[1243]A = \begin{bmatrix} 1 & 2 \\ 4 & 3 \end{bmatrix}.

det⁡(A)=(1)(3)−(2)(4)=3−8=−5\det(A) = (1)(3) - (2)(4) = 3 - 8 = -5.

adj(A)=[3−2−41]\text{adj}(A) = \begin{bmatrix} 3 & -2 \\ -4 & 1 \end{bmatrix}.

X=A−1=1det⁡(A)adj(A)=1−5[3−2−41]=15[−324−1]X = A^{-1} = \frac{1}{\det(A)} \text{adj}(A) = \frac{1}{-5} \begin{bmatrix} 3 & -2 \\ -4 & 1 \end{bmatrix} = \frac{1}{5} \begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}.

Therefore, the matrix XX is 15[−324−1]\frac{1}{5}\begin{bmatrix} -3 & 2 \\ 4 & -1 \end{bmatrix}.