Question

If ${\mathrm l}_1,\;{\mathrm m}_1,\;{\mathrm n}_1\;\mathrm{and}\;{\mathrm l}_2,\;{\mathrm m}_2,\;{\mathrm n}_2$ are DCs of two lines inclined to each other at an angle $\mathrm\theta$, then the DCs of the internal bisector of the angle between these lines are
$A.\;\dfrac{l_1+l_2}{2\sin{\displaystyle\dfrac\theta2}},\;\dfrac{m_1+m_2}{2\sin {\displaystyle\dfrac\theta2}},\;\dfrac{n_1+n_2}{2\sin{\displaystyle\dfrac\theta2}}\\\B.\;\dfrac{l_1+l_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{m_1+m_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{n_1+n_2}{2\cos{\displaystyle\dfrac\theta2}}\\\C.\;\dfrac{l_1-l_2}{2\sin{\displaystyle\dfrac\theta2}},\;\dfrac{m_1-m_2}{2\sin{\displaystyle\dfrac\theta2}},\;\dfrac{n_1-n_2}{2\sin{\displaystyle\dfrac\theta2}}\\\D.\;\dfrac{l_1-l_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{m_1-m_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{n_1-n_2}{2\cos{\displaystyle\dfrac\theta2}}$

Answer 1

Hint: This problem requires knowledge of direction cosines(DCs). A direction cosine is the cosine of the angle made by the vector/line with all the three axes. If p, q, r are the DCs of a line then $p^2 + q^2 + r^2 = 1$. Internal angle bisector is a line which divides the angle between two lines equally.

Complete step-by-step answer:

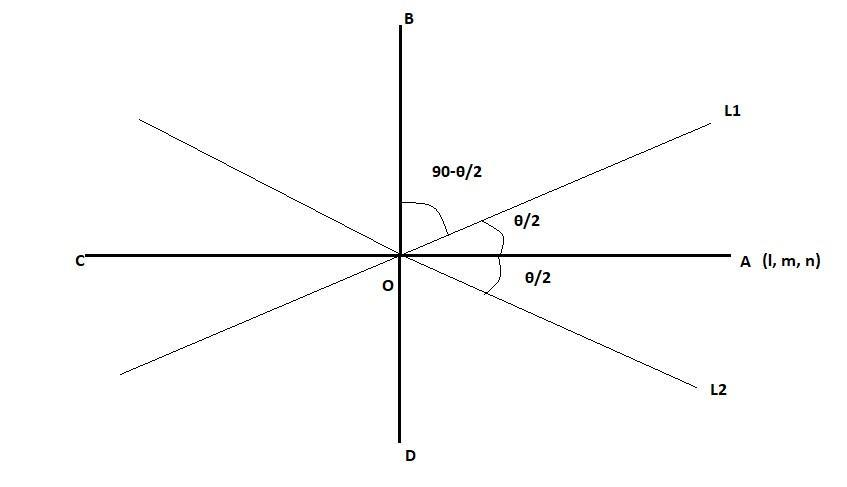
Let the two lines be $L_1$ and $L_2$. Let OA and OB be the two angle bisectors of the line. We have to find the DC of line OA(l, m, n). The formula for cosine of the angle between two lines in terms of the direction cosines is-
$\mathrm{lp}+\mathrm{mq}+\mathrm{nr}=\mathrm{cos\mathrm\alpha}$
Where l, m, n and p, q, r are DCs of the lines.

So, for lines L1 and OA,
$\cos\dfrac{\mathrm\theta}2={\mathrm{ll}}_1+{\mathrm{mm}}_1+ {\mathrm{nn}}_1\\\\\mathrm{Similarly}\;\mathrm{for}\;{\mathrm L}_2\;\mathrm{and}\;\mathrm{OA},\;\\\\\cos\dfrac{\mathrm\theta}2={\mathrm{ll}}_2+ {\mathrm{mm}}_2+{\mathrm{nn}}_2$
Adding these two equations, we get-
$2\cos\dfrac{\mathrm\theta}2=\mathrm l\left({\mathrm l}_1+{\mathrm l}_2\right)+\mathrm m\left({\mathrm m}_1+{\mathrm m}_2\right)+\mathrm n\left({\mathrm n}_1+{\mathrm n}_2\right)$
Cross-multiplying the equation we get-
$\dfrac{\mathrm l\left({\mathrm l}_1+{\mathrm l}_2\right)}{2\cos\dfrac{\mathrm\theta}2}+\dfrac{\mathrm m\left({\mathrm m}_1+{\mathrm m}_2\right)}{2\cos\dfrac{\mathrm\theta}2}+\dfrac{\mathrm n\left({\mathrm n}_1+{\mathrm n}_2\right)}{2\cos\dfrac{\mathrm\theta}2}=1=\cos0$

When looked closely, this equation represents the formula for finding the cosine between two lines with DCs l,m,n and $\dfrac{l_1+l_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{m_1+m_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{n_1+n_2}{2\cos{\displaystyle\dfrac\theta2}}$
But the angle between these lines is 0, this means that they coincide and their DCs are equal. This gives the required answer.
Hence,the correct option is B. $\dfrac{l_1+l_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{m_1+m_2}{2\cos{\displaystyle\dfrac\theta2}},\;\dfrac{n_1+n_2}{2\cos{\displaystyle\dfrac\theta2}}$

Note: In this type of problem diagrams are necessary to understand the question. If diagrams are drawn correctly and students know the formula, this problem can be solved with ease.