Question

If mass $M$ is $2{\text{ }}kg$ what is the tension in string AC? (in $N$)

Answer 1

First of all, we have to assume two different tensions in two different strings. Then by using the vertical component and horizontal component we will find the relation between the tension in string AC and BC. The total tension of both the strings will be equal to the weight of M.

Complete step by step answer:

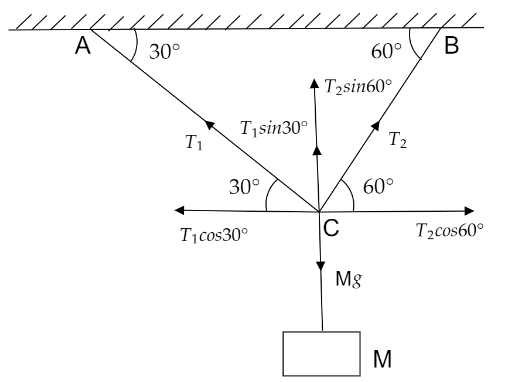
Let the tension in the string AC be ${T_1}$ and at BC be ${T_2}$.
We have to resolve the components of tensions of the string in AC and BC.
By equating in horizontal direction we get,
${T_1}\cos {30^ \circ } = {T_2}\cos {60^ \circ }$
Thus, we get the result as,
$\sqrt 3 {T_1} = {T_2} - - - - - \left( 1 \right)$
Given in the question M$= 2{\text{ }}kg$
By resolving the vertical components we get,
${T_1}\sin {30^ \circ } + {T_2}\sin {60^ \circ } = {\text{M}}g$
Now we get the equation as,
$\dfrac{{{T_1}}}{2} + \dfrac{{\sqrt 3 {T_2}}}{2} = 2 \times 10$
Substituting the values of ${T_2}$ from equation $\left( 1 \right)$ we get,
$4{T_1} = 40$
$\therefore {T_1} = 10$

So, the tension in the string AC is $10{\text{ }}N$.

Note: It must be noted that tension is a force which acts on the string. In the given diagram we use the vertically opposite angle concept to understand the tension forces more clearly. While resolving any component of force, the component which is attached to the angle is considered as $\cos$ component and the one which is away from the angle is the $\sin$ component. Tension is actually a force so it holds up the force exerted by the mass M.