Question

If $M$ is foot of the perpendicular from a point $P$ of the parabola ${{y}^{2}}=4ax$ to its directrix and $SPM$ is an equilateral triangle, where $S$ is the focus, then $SP$ is equal to
A. $a$
B. $2a$
C. $3a$
D. $4a$

Answer 1

First we will find the distance between the points $PS$ and $MS$. From the given data that $SPM$ is an equilateral triangle, we will do $PS=MS$ in order to get the value of $t$. By using the value of $t$ we will find the length of the $SP$.

Complete step by step answer:
Given that,
Equation of the parabola is ${{y}^{2}}=4ax$
Focus $\left( S \right)=\left( a,0 \right)$
The parabola with directrix $x=-a$ and having focus at $\left( a,0 \right)$ is given below

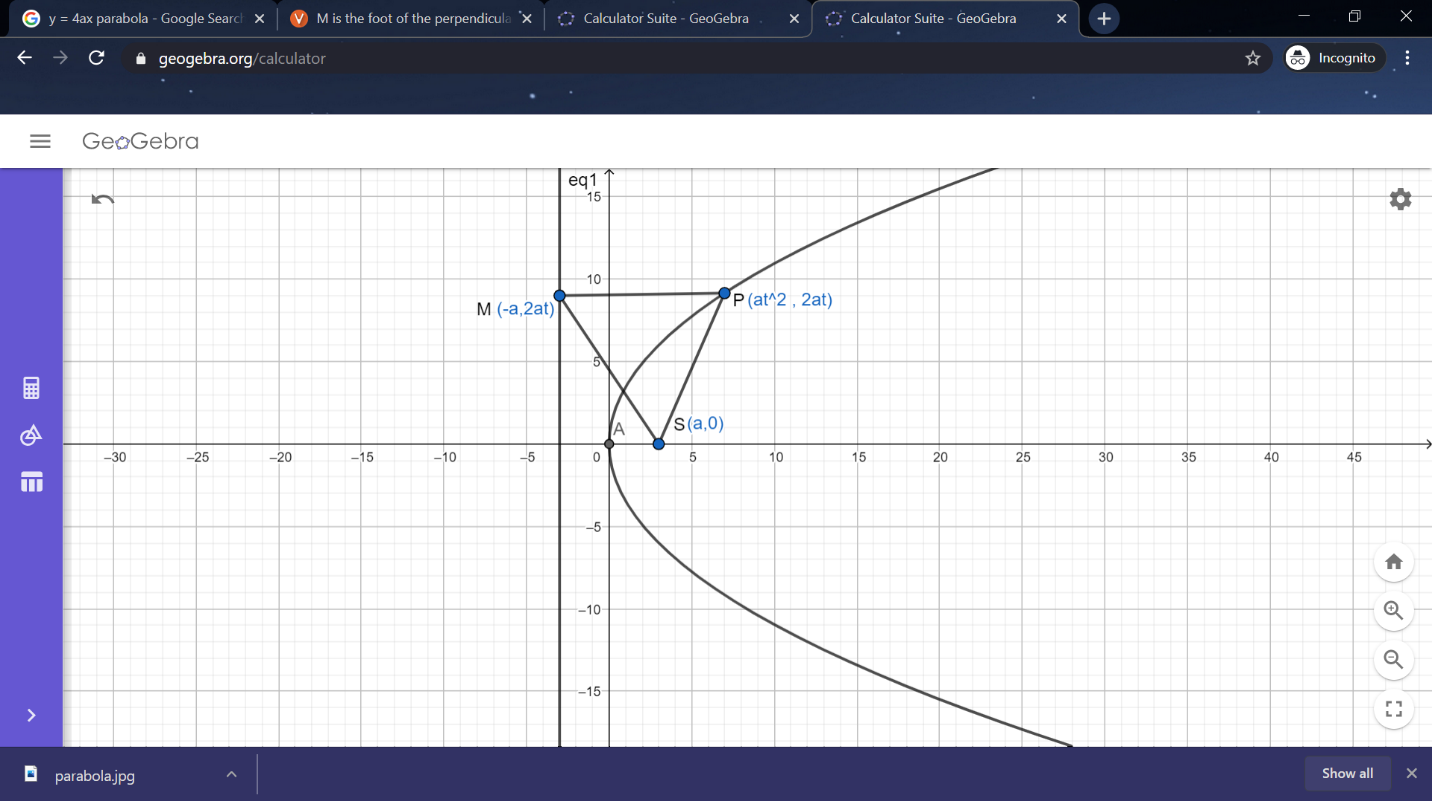
From the above diagram $P$ be the any point on the parabola and given by the coordinates $\left( a{{t}^{2}},2at \right)$
$M$ is the foot of the parabola so the coordinates of the point are $\left( -a,2at \right)$
Given that $PM$ is the perpendicular to the directrix.
Now the length of $PM$ is
$\begin{aligned} & PM=\sqrt{{{\left( a{{t}^{2}}+a \right)}^{2}}} \\\ & =a{{t}^{2}}+a \end{aligned}$
And the length of $MS$ is
$\begin{aligned} & MS=\sqrt{{{\left( -a-a \right)}^{2}}+{{\left( 2at-0 \right)}^{2}}} \\\ & =\sqrt{4{{a}^{2}}+4{{a}^{2}}{{t}^{2}}} \\\ & =2a\sqrt{1+{{t}^{2}}} \end{aligned}$
Given that $\Delta PMS$ is an equilateral triangle as shown in figure

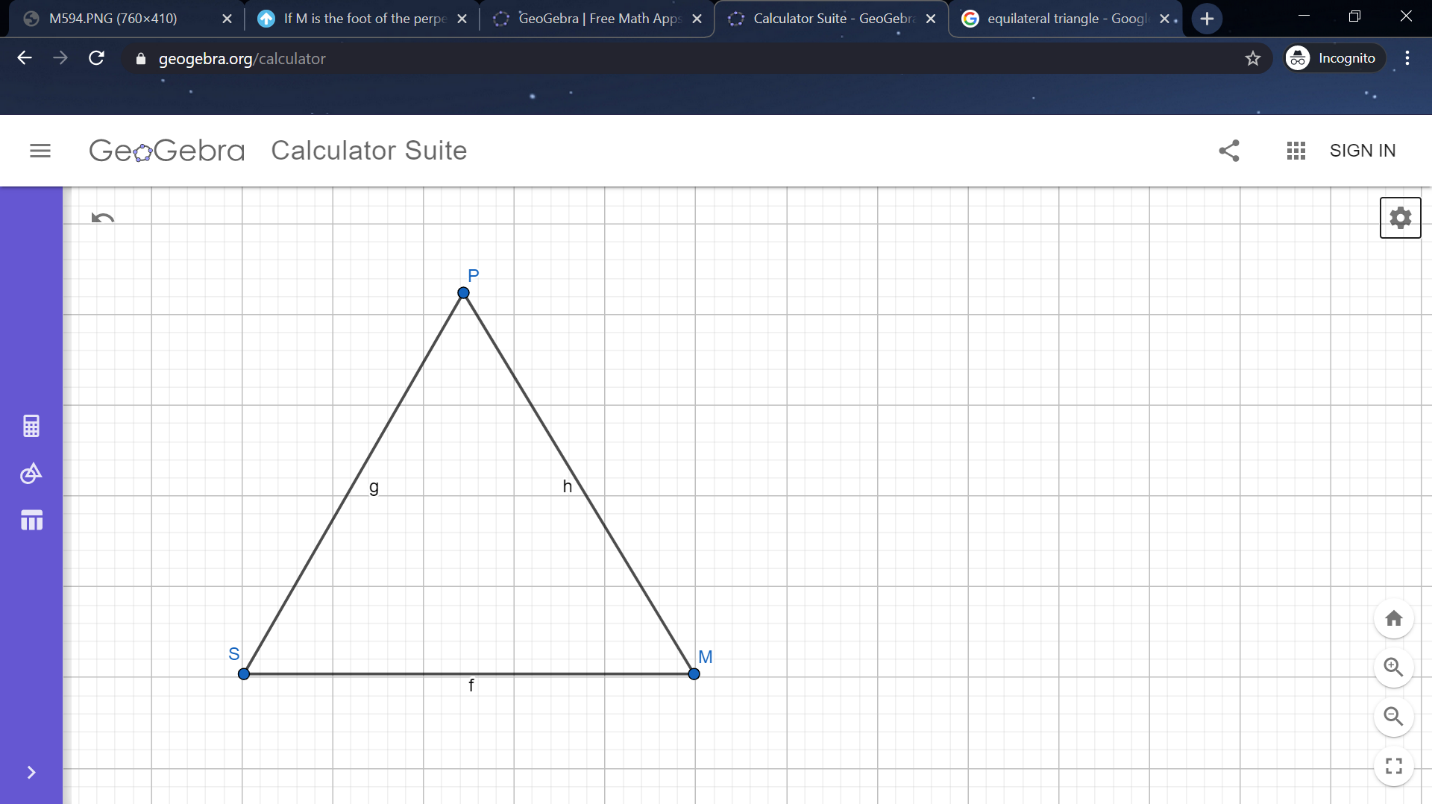
In an equilateral triangle all sides have same length then
$PM=MS$
Squaring on both sides and substituting the value of $PM$ and $MS$ then
$\begin{aligned} & {{\left( PM \right)}^{2}}={{\left( MS \right)}^{2}} \\\ & {{\left( a{{t}^{2}}+a \right)}^{2}}=4{{a}^{2}}\left( 1+{{t}^{2}} \right) \\\ & {{t}^{4}}-2{{t}^{2}}-3=0 \\\ & {{t}^{2}}=3;-1\left( \text{not possible,so} \right) \\\ & {{t}^{2}}=3 \end{aligned}$
So, the value of $PS$ is
$\begin{aligned} & PS=PM \\\ & =a\left( 3 \right)+a \\\ & =4a \end{aligned}$

So, the correct answer is “Option D”.

Note: Please remember the coordinates of the different points on the parabola like focus of the parabola, point on the parabola and perpendicular foot on to the directrix of the parabola. Don’t write $PS=a\left( 1+{{t}^{2}} \right)$ in ${{\left( PS \right)}^{2}}={{\left( MS \right)}^{2}}$ why because if you substitute $PS=a\left( 1+{{t}^{2}} \right)$ then the term $1+{{t}^{2}}$ is canceled and we don’t get the value of $t$. So, leave the value of $PS$ as $a{{t}^{2}}+a$.