Question

If $\log_{a} 3=2$ and $\log_{b} 8=3$ then $\log_{b} a$ is.

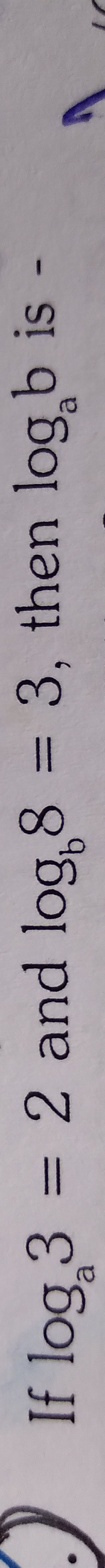
Answer 1

\frac{1}{2} \log_{2} 3

Answer 2

1. Convert logarithmic form to exponential form:

   • From $\log_{a} 3 = 2$, we get $a^2 = 3$. Since the base of a logarithm must be positive, $a = \sqrt{3} = 3^{1/2}$.
   • From $\log_{b} 8 = 3$, we get $b^3 = 8$. Taking the cube root, $b = 2$.

2. Substitute the values of $a$ and $b$ into $\log_{b} a$:

   • We need to find $\log_{b} a = \log_{2} (3^{1/2})$.

3. Apply logarithm properties:

   • Using the power rule for logarithms, $\log_x (y^z) = z \log_x y$, we simplify: $\log_{2} (3^{1/2}) = \frac{1}{2} \log_{2} 3$.

Therefore, $\log_{b} a = \frac{1}{2} \log_{2} 3$.