Solveeit Logo
Login

Question

Question: If \({\log _{0.3}}({\text{x - 1) < lo}}{{\text{g}}_{0.09}}{\text{(x - 1) }}\), then x lies in the in...

If log⁡0.3(x - 1) < log0.09(x - 1) {\log _{0.3}}({\text{x - 1) < lo}}{{\text{g}}_{0.09}}{\text{(x - 1) }}, then x lies in the interval
A. (2, ∞\infty )
B. (1,2)
C. (-2, -1)
D. None of these

Explanation

Solution

Hint: to solve this problem, we have to check whether the logarithmic function is an increasing or decreasing function. So, we will make the graph of log x and then with the help of graph we will solve the given inequality. We will also use some properties of logarithmic function. We will use the property logbca=1clogbalog_{b^c}a = \dfrac{1}{c} log_{b}a and logmn=nlogmlog{m^n} = nlogm.

Complete step-by-step answer:

Now, we will first draw the graph of log x.

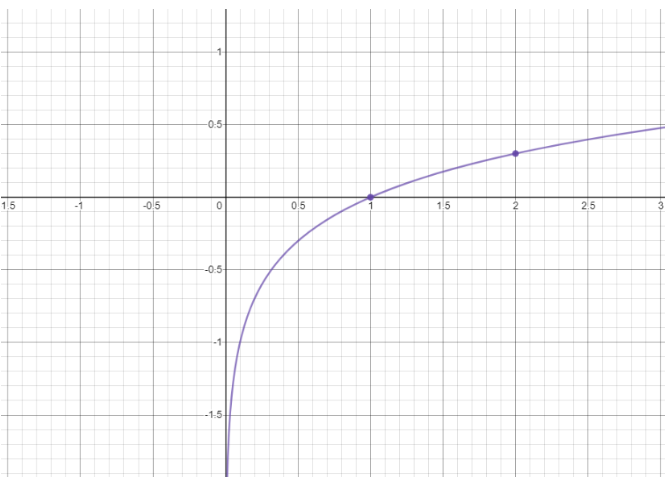
From the graph, we can see that log x is an increasing function, which means the value of log x increases as the value of x increases.
Now, for an increasing function the inequality remains the same, but for a decreasing function, the given inequality reverses.
Given inequality is
log⁡0.3(x - 1) < log0.09(x - 1) {\log _{0.3}}({\text{x - 1) < lo}}{{\text{g}}_{0.09}}{\text{(x - 1) }}
Now, above equation can be written as
log⁡0.3(x - 1) < 12log⁡0.3(x - 1){\log _{0.3}}({\text{x - 1) < }}\dfrac{1}{2}{\log _{0.3}}({\text{x - 1)}} as log⁡bca = 1clog⁡ba{\log _{{{\text{b}}^{\text{c}}}}}{\text{a = }}\dfrac{1}{{\text{c}}}{\log _{\text{b}}}{\text{a}}
⇒\Rightarrow log⁡0.3(x - 1) < log0.3(x - 1)12{\log _{0.3}}({\text{x - 1) < l}}o{g_{0.3}}{({\text{x - 1)}}^{\dfrac{1}{2}}} as log⁡mn = nlogm\log {{\text{m}}^{\text{n}}}{\text{ = nlogm}}
Taking anti – log both sides, we get
(x - 1) < (x - 1)12({\text{x - 1) < }}{({\text{x - 1)}}^{\dfrac{1}{2}}}
Squaring both sides,
(x - 1)2 < (x - 1){({\text{x - 1)}}^2}{\text{ < }}({\text{x - 1)}}
Solving the above equation by opening the square and taking (x – 1) to the left – hand side, we get
(x - 1)(x - 2) < 0({\text{x - 1)(x - 2) < 0}}
So, the interval is (1,2)
So, x lies in the interval (1,2). So, option (B) is correct.

Note: When we come up with such types of questions, which includes inequality, we have to first draw the graph to find the nature of function, whether it is increasing or decreasing function. Then we will apply properties of the given function to solve the inequality and to find the interval which satisfies the given inequality.