Question

If linear density of a rod of length 3 m varies as then the position of the centre of gravity of the rod is :

• A. $\frac{7}{3}m$
• B. $\frac{12}{7}m$
• C. $\frac{10}{7}m$
• D. $\frac{9}{7}m$

Answer 1

Answer: (B)

$\frac{12}{7}m$

Answer 2

Linear density of the rod varies with distance

$\frac{dm}{dx} = \lambda$ (given) $\Rightarrow \mspace{6mu}\mspace{6mu} dm = \lambda dx$

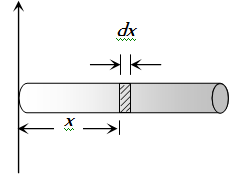
Position of centre of mass

$x_{cm} = \frac{\int_{}^{}{dm\mspace{6mu} \times \mspace{6mu} x}}{\int_{}^{}{dm\mspace{6mu}}} = \frac{\int_{0}^{3}{(\lambda\mspace{6mu} dx) \times x}}{\int_{0}^{3}{\lambda dx}} = \frac{\int_{0}^{3}{(2\mspace{6mu} + x) \times xdx}}{\int_{2}^{3}{(2 + x)\mspace{6mu} dx}} = \frac{\left\lbrack x^{2} + \frac{x^{3}}{3} \right\rbrack_{0}^{3}}{\left\lbrack 2x + \frac{x^{3}}{2} \right\rbrack_{0}^{3}}$

$= \frac{9 + 9}{6 + \frac{9}{2}} = \frac{36}{21} = \frac{12}{7}m$ 23