Question

If line makes an angle $120{}^\circ$ and $60{}^\circ$ with the positive directions of X and Z axes respectively then the angle made by the line with positive Y-direction is
(a) $150{}^\circ$
(b) $60{}^\circ$
(c) $135{}^\circ$
(d) $120{}^\circ$

Answer 1

First, we will be using the concept of direction of the cosine vector. So, we will understand that first. Then we will be using its property which is given as the sum of the squares of the direction cosines is equal to one. In Mathematical terms, it is written as ${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1$ . We are given values of $\alpha =120{}^\circ$ , $\gamma =60{}^\circ$ . On putting values and solving, we will get the answer.

Complete step-by-step solution:
Here, we will use the Directions of the Cosine vector. So, we will understand the concept of this. The direction cosines of the vector $\vec{a}$ are the cosines of the angles that the vector forms with the coordinate axes. Here, we are given an angle of 3 directions and the remaining 1 we have to find. So, for this, we will use the concept that the sum of the squares of the direction cosines is equal to one.
We will draw the direction of the figure for direction cosines of a vector for a three-dimensional vector.

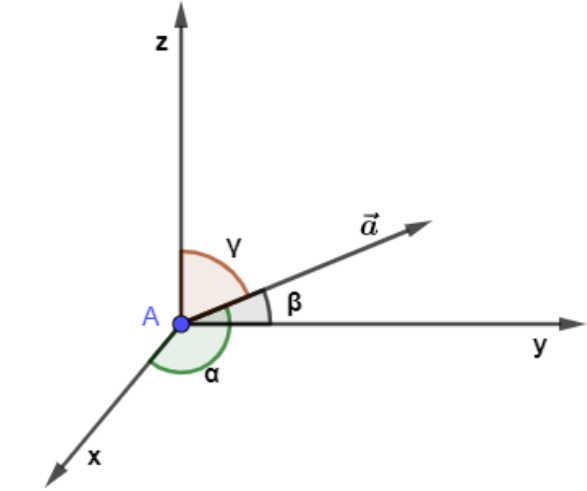
The direction cosine of vector \vec{a}=\left\\{ {{a}_{x}};{{a}_{y}};{{a}_{z}} \right\\} can be found as $\cos \alpha =\dfrac{{{a}_{x}}}{\left| \overline{a} \right|};\cos \beta =\dfrac{{{a}_{y}}}{\left| \overline{a} \right|};\cos \gamma =\dfrac{{{a}_{z}}}{\left| \overline{a} \right|}$. Also, the sum of the squares of the direction cosines is equal to one which is written as ${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1$ .
We are given that $\alpha =120{}^\circ$ , $\gamma =60{}^\circ$ . On substituting the value, we get as
${{\cos }^{2}}120{}^\circ +{{\cos }^{2}}\beta +{{\cos }^{2}}60{}^\circ =1$
This can also be written as
${{\cos }^{2}}\left( 180-60{}^\circ \right)+{{\cos }^{2}}\beta +{{\cos }^{2}}60{}^\circ =1$
We know that $\cos \left( 180-60{}^\circ \right)=-\cos 60{}^\circ$ and value of $\cos 60{}^\circ =\dfrac{1}{2}$ . Thus, on putting values we get as
$-{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}\beta +{{\cos }^{2}}60{}^\circ =1$
${{\left( -\dfrac{1}{2} \right)}^{2}}+{{\cos }^{2}}\beta +{{\left( \dfrac{1}{2} \right)}^{2}}=1$
On solving, we get as
$\dfrac{1}{4}+{{\cos }^{2}}\beta +\dfrac{1}{4}=1$
${{\cos }^{2}}\beta +\dfrac{1}{2}=1$
On taking constant term on right side, we get as
${{\cos }^{2}}\beta =1-\dfrac{1}{2}=\dfrac{1}{2}$
On taking square root on both side, we get as
$\cos \beta =\pm \dfrac{1}{\sqrt{2}}$
Thus, on taking cos inverse on both side, we get answer as
$\beta ={{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)or{{\cos }^{-1}}\left( -\dfrac{1}{\sqrt{2}} \right)$
We know that ${{\cos }^{-1}}\left( \dfrac{1}{\sqrt{2}} \right)=45{}^\circ$ and ${{\cos }^{-1}}\left( -\dfrac{1}{\sqrt{2}} \right)=180-45=135{}^\circ$ . So, these both are the answer. So, the option $135{}^\circ$ is given.

Hence, option (c) is the correct answer.

Note: This cosine rule we can directly apply but if we convert this formula ${{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1$ into sin function using the formula ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ and replacing cos function to sin function, we will get the same answer on solving. Few steps will be more to solve but ultimately it will give the same answer. We get as $1-{{\sin }^{2}}\alpha +1-{{\sin }^{2}}\beta +1-{{\sin }^{2}}\gamma =1$ . On substituting the values and solving we will get an answer.