Question
Question: If $\lim_{x\to 0} (1+ax+bx^2)^{2/x} = e^e$, then...
If limx→0(1+ax+bx2)2/x=ee, then
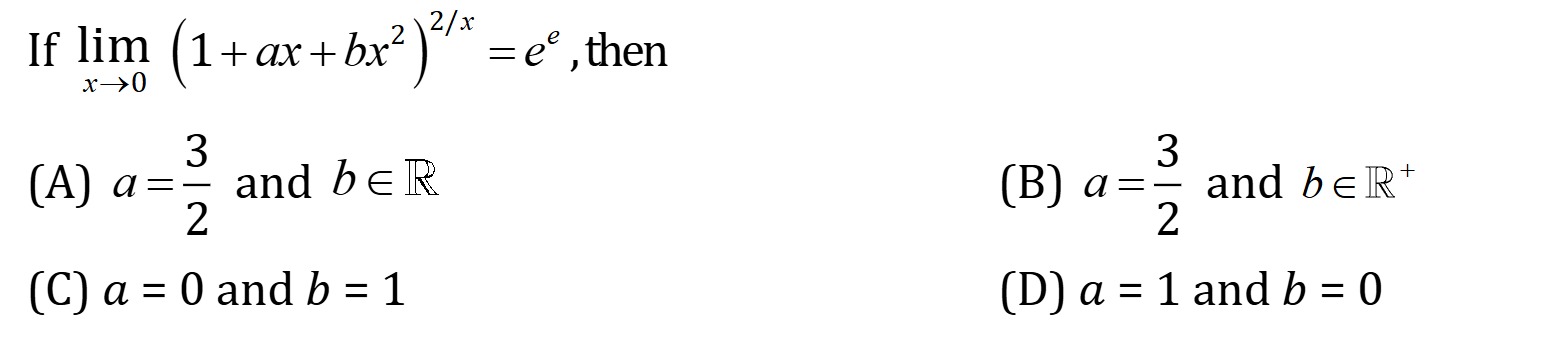
a=3/2 and b in R
a=3/2 and b in R+
a=0 and b=1
a=1 and b=0
The provided options do not match the exact question. If the question intended the limit to be e3, then option (A) would be correct. Based on the exact question limx→0(1+ax+bx2)2/x=ee, we find a=e/2 and b∈R. Since this is not an option, and assuming there's a typo in the question and it should be e3, then a=3/2 and b∈R is the intended answer.
Solution
The limit is of the indeterminate form 1∞. We can evaluate it using the formula limx→c(f(x))g(x)=elimx→cg(x)(f(x)−1) or by using Taylor series expansion.
Let L=limx→0(1+ax+bx2)2/x. We can write L as: L=exp(limx→0x2ln(1+ax+bx2))
Now, we evaluate the limit in the exponent: limx→0x2ln(1+ax+bx2) As x→0, ax+bx2→0. We use the Taylor expansion of ln(1+u) around u=0, which is ln(1+u)=u−2u2+O(u3). Let u=ax+bx2. ln(1+ax+bx2)=(ax+bx2)−2(ax+bx2)2+O((ax+bx2)3) ln(1+ax+bx2)=ax+bx2−2a2x2+2abx3+b2x4+O(x3) ln(1+ax+bx2)=ax+(b−2a2)x2+O(x3) Substitute this back into the exponent's limit: limx→0x2(ax+(b−2a2)x2+O(x3)) =limx→02(a+(b−2a2)x+O(x2)) =2(a+0)=2a So, the limit L is e2a.
The problem states that L=ee. e2a=ee Equating the exponents, we get: 2a=e⟹a=2e The value of b does not affect the limit as x→0, because the term involving b in the Taylor expansion of the logarithm is multiplied by x2, and then by 2/x, resulting in a term proportional to x, which vanishes as x→0. Thus, b can be any real number (b∈R).
The derived values are a=e/2 and b∈R. However, a=e/2 is not present in any of the given options. This strongly suggests a typo in the question, where ee was likely intended to be e3. This is a common type of typo in limit problems of this nature.
If we assume the question intended the limit to be e3: If limx→0(1+ax+bx2)2/x=e3, then: e2a=e3 Equating the exponents: 2a=3⟹a=23 As established before, the value of b does not affect the limit. Therefore, b can be any real number (b∈R).
Under this assumption, we have a=3/2 and b∈R. This matches option (A).
