Question

If $\lim_{x \to \lambda} \left(2-\frac{\lambda}{x}\right)^{\lambda \tan\left(\frac{\pi x}{2\lambda}\right)} = \frac{1}{e}$, then $\lambda$ is equal to -

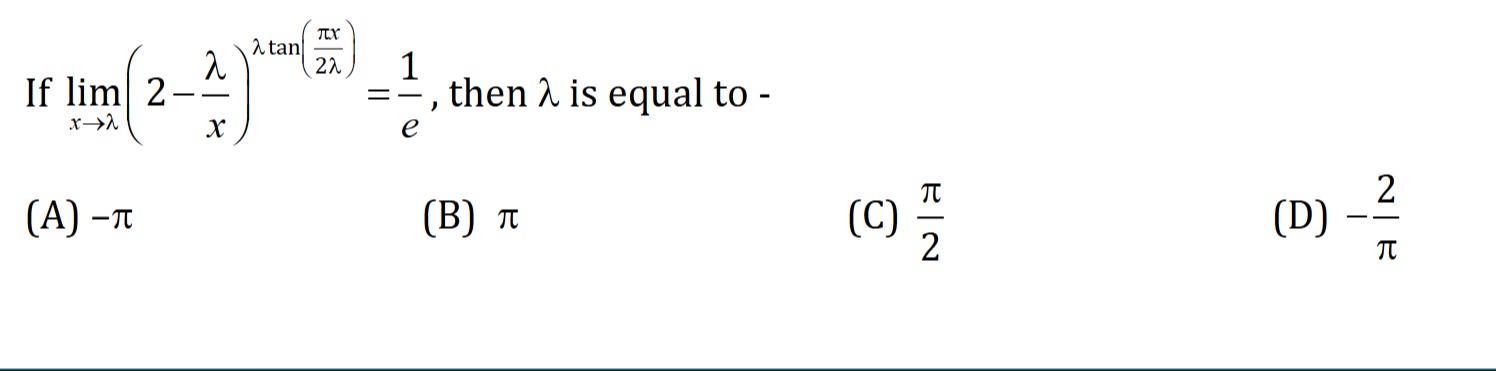
• A. $-\pi$
• B. $\pi$
• C. $\frac{\pi}{2}$
• D. $-\frac{2}{\pi}$

Answer 1

Answer: (C)

$\frac{\pi}{2}$

Answer 2

The limit is of the form $1^\infty$. The given limit $\lim_{x \to \lambda} [f(x)]^{g(x)}$ can be evaluated as $e^{\lim_{x \to \lambda} g(x) [f(x)-1]}$. Here, $f(x) = 2 - \frac{\lambda}{x}$ and $g(x) = \lambda \tan\left(\frac{\pi x}{2\lambda}\right)$. The limit of the exponent is $L = \lim_{x \to \lambda} \lambda \tan\left(\frac{\pi x}{2\lambda}\right) \left(1 - \frac{\lambda}{x}\right) = \lim_{x \to \lambda} \frac{\lambda (x - \lambda)}{x \cot\left(\frac{\pi x}{2\lambda}\right)}$. Applying L'Hopital's Rule to the $\frac{0}{0}$ form, we get $L = \frac{\lambda}{\cot(\frac{\pi x}{2\lambda}) - x \csc^2(\frac{\pi x}{2\lambda}) \frac{\pi}{2\lambda}} \Big|_{x=\lambda}$. Evaluating this limit gives $L = \frac{\lambda}{0 - \lambda(1)^2(\frac{\pi}{2\lambda})} = \frac{\lambda}{-\pi/2} = -\frac{2\lambda}{\pi}$. Given limit is $e^L = \frac{1}{e} = e^{-1}$, so $L = -1$. Equating the exponent limits: $-\frac{2\lambda}{\pi} = -1 \implies \lambda = \frac{\pi}{2}$.