Question

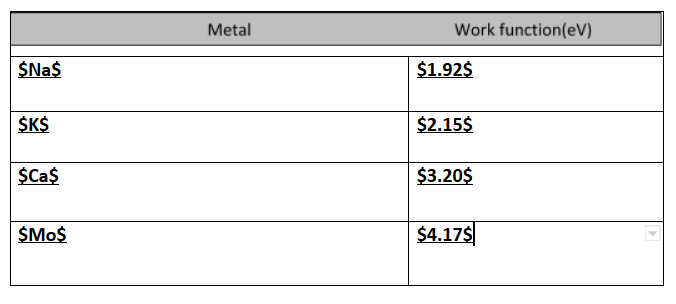
If light of wavelength $412.5nm$ is incident on each of the metals given below, which ones will show photoelectric emission and why?

Answer 1

Hint :Photoelectric effect is the emission of electrons when a electromagnetic radiation of a certain minimum frequency falls on the surface of a metal. A certain minimum frequency is required for rejecting the electron. For photoelectric emission $h\nu = W + K.E$.

Complete answer:
When light of a certain minimum frequency hits the metal surface the electrons will be just ejected. This minimum frequency required is called threshold frequency ${\nu _0}$. .The value $h{\nu _0}$ is called the work function. This work function varies according to each metal surface. The light falling on the metal surface therefore should be greater than the threshold frequency.
If a electromagnetic radiation of frequency $\nu$ which is greater than the threshold frequency falls on the metal surface the additional energy will be given to the electron as kinetic energy. This can be written in equation form as $h\nu = h{\nu _0} + KE$. Here KE represents the kinetic energy.
Here given that light falling gas a wavelength of $412.5nm$ .Therefore using equation $\nu = \dfrac{c}{\lambda }$ we get the frequency of the incident light is
$= \dfrac{{3 \times {{10}^8}}}{{412.5 \times {{10}^ - }9}}$
$= 7.27 \times {10^{14}}$
Calculating its energy and converting it into electron volts ($1J = 6.242 \times {10^{18}}eV)$
$E = h\nu = 6.626 \times {10^{ - 34}} \times {\text{ }}7.27 \times {10^{14}} \times 6.6242 \times {10^{18}}$
$= 3eV$
Therefore all the metals having a work function less than 3eV will be ejected.$Na$ and $K$ which has a work function of $1.92$ and $2.15$ will eject electrons.
Note When the wavelength of the incident light is given its energy in electron volts is directly given by the equation (by substituting all other constant values)$E = \dfrac{{1240}}{{\lambda (in\;nm)}}eV$
Substituting the wavelength here we get the energy in electron volt is equal to $3eV$.
Memorising this equation will help to solve the question faster.