Question

If $\left( \dfrac{3}{2},\dfrac{5}{2} \right)$ is the midpoint of the line segment intercepted by a line between axes, then the equation of the line is
1. $5x+3y+15=0$
2. $3x+5y+15=0$
3. $5x+3y-15=0$
4. $3x+5y-15=0$

Answer 1

In this problem we need to calculate the equation of the line according to the given data. We will first consider the intersects of the required line as $a$ and $b$. Now the midpoint of the line joining the intersection is given by $\left( \dfrac{3}{2},\dfrac{5}{2} \right)$. From this we will calculate the values of intercepts. After having the intercepts of the line the equation of the line in intercept form is given by $\dfrac{x}{a}+\dfrac{y}{b}=1$ .

Complete step by step answer:
Given, $\left( \dfrac{3}{2},\dfrac{5}{2} \right)$ is the midpoint of the line segment intercepted by a line between axes.
Let the intercepts of the required line are $\left( a,0 \right)$ and $\left( 0,b \right)$.

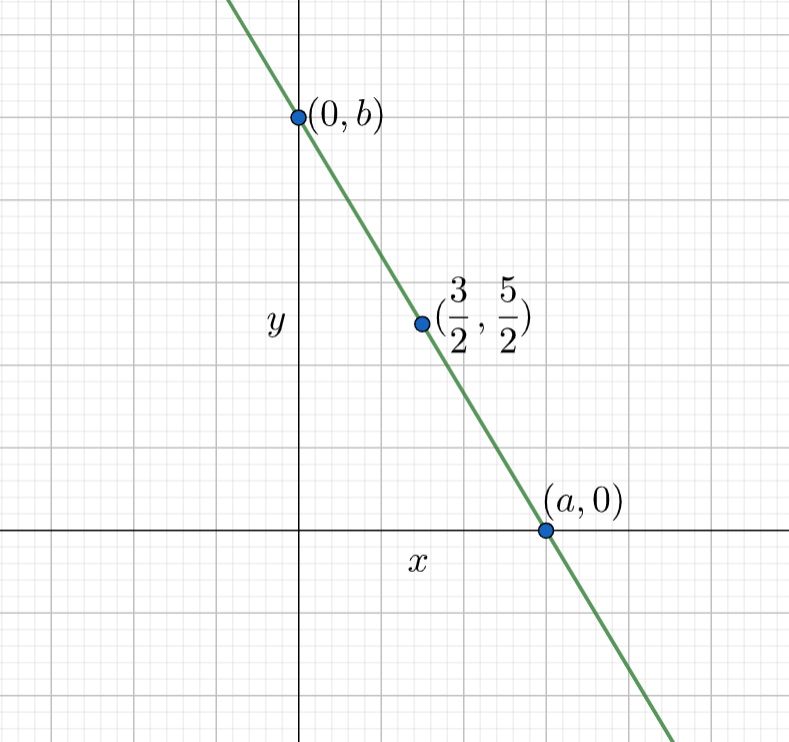
If the point $\left( \dfrac{3}{2},\dfrac{5}{2} \right)$ is the midpoint of the line joining the points $\left( a,0 \right)$ and $\left( 0,b \right)$, then we can write
$\dfrac{a+0}{2}=\dfrac{3}{2}$ and $\dfrac{0+b}{2}=\dfrac{5}{2}$
Simplifying the above equations, we will get
$a=3$ and $b=5$ .
So, we have the intercepts of the required line as $a=3$ and $b=5$ .
Now the equation of the line by using the intercept form, with intercepts $a=3$ and $b=5$ can be written as
$\begin{aligned} & \dfrac{x}{3}+\dfrac{y}{5}=1 \\\ & \Rightarrow \dfrac{5x+3y}{3\left( 5 \right)}=1 \\\ & \Rightarrow 5x+3y=15 \\\ & \Rightarrow 5x+3y-15=0 \\\ \end{aligned}$

So the equation of the line is $5x+3y-15=0$ .

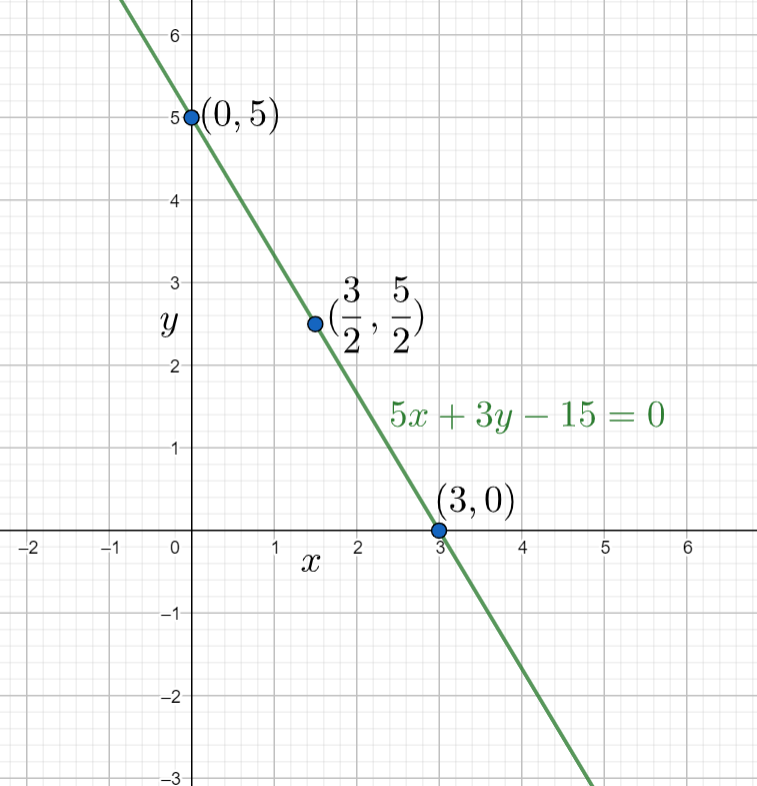
So, the correct answer is “Option 3”.

Note: In this problem we have used the intercept of the line to get the equation of the line. We can also use the slope intercept form of the line which is given by $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$ to get the equation of the required line. Here we need to calculate the slope of the line additionally. So we haven’t followed this procedure.