Question

If $\left( {{\alpha }^{2}},\alpha -2 \right)$ be a point interior to the region of the parabola ${{y}^{2}}=2x$ bounded by the chord joining the points (2, 2) and (8, -4) then P belongs to the interval
(a)$-2+2\sqrt{2}<\alpha <2$
(b)$\alpha >-2+2\sqrt{2}$
(c)$\alpha >-2-2\sqrt{2}$
(d)None of these

Answer 1

Hint: Any point $\left( {{x}_{1}},{{y}_{1}} \right)$ lying inside of any conic S = 0 will satisfy the equation, $S\left( {{x}_{1}},{{y}_{1}} \right)<0$, where S is the standard form of conic. Put (0, 0) to the chord and determine the sign of it and hence, according to it the sign will change, while putting $\left( {{\alpha }^{2}},\alpha -2 \right)$ to the equation of chord. If they point to chords and use ‘< 0’ and vice – versa for positive sign (> 0). Solve the two inequalities calculated with the help of two conditions mentioned above. Take their intersection to get the answer.

Complete step-by-step answer:
Here, we have to find the interval for $\alpha$, if it is given that $\left( {{\alpha }^{2}},\alpha -2 \right)$ is a point lying in the region of the parabola ${{y}^{2}}=4x$ bounded by the chord joining the points (2, 2) and (8, -4).
So, diagram with the help of the given informations can be given as,

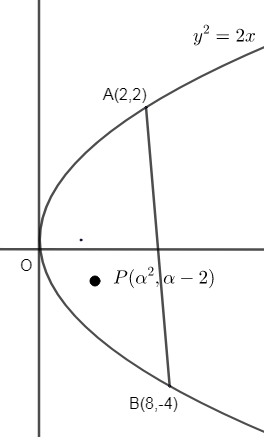
Let us find out the equation of the line passing through the points A and B.
We know equation of a line with given two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ as,
$y-{{y}_{1}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\left( x-{{x}_{1}} \right)-(i)$
Now, we have two points A and B, so, we can get the equation of line passing through A and B as,

& y-2=\dfrac{-4-2}{8-2}\left( x-2 \right) \\\ & y-2=\dfrac{-6}{6}\left( x-2 \right) \\\ & y-2=-1\left( x-2 \right) \\\ & y-2=-x+2 \\\ & x+y=4 \\\ \end{aligned}$$ Or $$x+y-4=0-(ii)$$ Now, as $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ is lying inside the region of parabola. And we know if any point lies inside the curve, S = 0, then $$S\left( {{x}_{1}},{{y}_{1}} \right)<0-(iii)$$ Where $$\left( {{x}_{1}},{{y}_{1}} \right)$$ is a point lying inside the curve S. So, as equation of parabola given is, $${{y}^{2}}-2x=0-(iv)$$ Now, as $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ is lying inside the curve (iv). So, using equation (iii), we get, $$\begin{aligned} & {{\left( \alpha -2 \right)}^{2}}-2{{\alpha }^{2}}<0 \\\ & {{\alpha }^{2}}+4-4\alpha -2{{\alpha }^{2}}<0 \\\ & -{{\alpha }^{2}}-4\alpha +4<0 \\\ \end{aligned}$$ Multiplying with -1 will change the above inequality. So, we get, $${{\alpha }^{2}}+4\alpha -4>0-(v)$$ Now, we can find roots of equation $${{\alpha }^{2}}+4\alpha -4=0$$ by using the quadratic formula given for any quadratic $$a{{x}^{2}}+bx+c=0$$ as, $$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}-(vi)$$ Hence, roots of equation (v), we get, $$\begin{aligned} & =\dfrac{-4\pm \sqrt{16-4\times \left( -4 \right)}}{2\times 1} \\\ & =\dfrac{-4\pm \sqrt{16+16}}{2} \\\ & =\dfrac{-4\pm \sqrt{32}}{2}=\dfrac{-4\pm 4 \sqrt{2}}{2} \\\ & =-2\pm 2\sqrt{2} \\\ \end{aligned}$$ Now, we can write the equation (v) as, $$\left( \alpha -\left( -2+2\sqrt{2} \right) \right)\left( \alpha +\left( -2-2\sqrt{2} \right) \right)>0$$ We know, If $$\left( x-a \right)\left( x-b \right)>0$$ Then, $$x\in \left( -\infty ,a \right)\cup \left( b,\infty \right)$$, where (a < b). So, we get, $$\begin{aligned} & \left( \alpha -\left( -2+2\sqrt{2} \right) \right)\left( \alpha -\left( -2-2\sqrt{2} \right) \right)>0 \\\ & \alpha \in \left( -\infty ,-2-2\sqrt{2} \right)\cup \left( -2+2\sqrt{2},\infty \right)-(vii) \\\ \end{aligned}$$ Now, as the point $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ is lying left to the equation represented by line segment AB. i.e. $$x+y-4=0$$. Now, as we can observe (0, 0) is also lying on the left hand side of the line, so the sign given by putting (0, 0) to (x + y -4) is same as sign by putting $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ to $$x+y-4=0$$. So, putting (0, 0) to the line $$x+y-4=0$$, we get, $$0+0-4=-4<0$$ Hence, $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ will also give less than 0 by putting it to $$x+y-4=0$$. So, we get, $$\begin{aligned} & {{\alpha }^{2}}+\alpha -2-4<0 \\\ & {{\alpha }^{2}}+\alpha -6<0 \\\ \end{aligned}$$ We can factorize the equation as, $$\begin{aligned} & {{\alpha }^{2}}+3\alpha -2\alpha -6<0 \\\ & \alpha \left( \alpha +3 \right)-2\left( \alpha +3 \right)<0 \\\ & \left( \alpha -2 \right)\left( \alpha +3 \right)<0 \\\ \end{aligned}$$ We know, If $$\left( x-a \right)\left( x-b \right)<0$$ $$x\in \left( a,b \right)$$, where a < b Hence, we get, $$\begin{aligned} & \left( \alpha -2 \right)\left( \alpha +3 \right)<0 \\\ & \left( \alpha -2 \right)\left( \alpha -\left( -3 \right) \right)<0 \\\ & \alpha \in \left( -3,2 \right)-(viii) \\\ \end{aligned}$$ Now, we know the range of $$\alpha $$ with respect to parabola as well as with respect to line AB as well. But we need to find ‘$$\alpha $$’, where both conditions are satisfied. So, we need to take the intersection of the ranges of $$\alpha $$ from equations (vii) and (viii).  Now, we can observe from the above representation of intervals, we get the intersection of $$\alpha $$ as, $$\alpha \in \left( -2+2\sqrt{2},2 \right)$$ Or $$-2+2\sqrt{2}<\alpha <2$$ Hence, option (a) is the correct answer. Note: One may go wrong if he / she put $$\left( {{\alpha }^{2}},\alpha -2 \right)$$ to the equation $$2x-{{y}^{2}}=0$$ and put the same inequality i.e. ‘<’. Here, we need to use only standard form of curves i.e. $${{y}^{2}}-4ax=0$$ or $$ax+by+c=0$$, not any other form, otherwise, we need to change the inequality as well according to the equation. One may use a number line for the inequalities $$\left( x-a \right)\left( x-b \right)<0$$ or $$\left( x-a \right)\left( x-b \right)>0$$ as well. We used the direct results of these inequalities in the solution. So, try to remember the results for future reference with these kinds of questions.