Solveeit Logo
Login

Question

Question: If \[\left( { - 4,3} \right)\] and \[\left( {4,3} \right)\] are two vertices of an equilateral trian...

If (−4,3)\left( { - 4,3} \right) and (4,3)\left( {4,3} \right) are two vertices of an equilateral triangle, find the co-ordinates of the third vertex, given that the origin lies in the (i) interior, (ii) exterior of the triangle.

Explanation

Solution

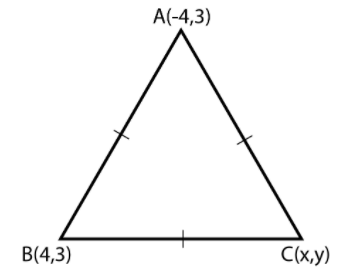
Let the equilateral triangle be ΔABC\Delta ABC with vertices A(−4,3), B(4,3)A\left( { - 4,3} \right), {\text{ }}B\left( {4,3} \right) and C(x,y)C\left( {x,y} \right).

First, find the distance AB, BC and Ac using the distance formula d=(x1−x2)2+(y1−y2)2d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} .
Now, as it is given, the triangle is an equilateral triangle, AB=BC=ACAB = BC = AC .
Find AB and then by BC=ACBC = AC and AC=ABAC = AB find the linear relations in terms of x and y.
Thus, find x and y which will give the coordinates of the third vertex.

Complete step by step solution:
Let the equilateral triangle be ΔABC\Delta ABC with vertices A(−4,3), B(4,3)A\left( { - 4,3} \right), {\text{ }}B\left( {4,3} \right) and C(x,y)C\left( {x,y} \right) .
Now, let us first find the distance between the points A and B using the distance formula AB=(x1−x2)2+(y1−y2)2AB = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}} .
⇒AB=(−4−4)2+(3−3)2\Rightarrow AB = \sqrt {{{\left( { - 4 - 4} \right)}^2} + {{\left( {3 - 3} \right)}^2}}
=(−8)2+0 =64=8 = \sqrt {{{\left( { - 8} \right)}^2} + 0} \\\ = \sqrt {64} =8
So, let us now find the distance between B and C.
⇒BC=(4−x)2+(3−y)2\Rightarrow BC = \sqrt {{{\left( {4 - x} \right)}^2} + {{\left( {3 - y} \right)}^2}}
Also, the distance between A and C will be
AC=(−4−x)2+(3−y)2AC = \sqrt {{{\left( { - 4 - x} \right)}^2} + {{\left( {3 - y} \right)}^2}}
Now, as it is an equilateral triangle, the distances AB, BC and AC must be equal.
So, BC=ACBC = AC
⇒(4−x)2+(3−y)2=(−4−x)2+(3−y)2\Rightarrow \sqrt {{{\left( {4 - x} \right)}^2} + {{\left( {3 - y} \right)}^2}} = \sqrt {{{\left( { - 4 - x} \right)}^2} + {{\left( {3 - y} \right)}^2}}
Squaring both sides

⇒(4−x)2+(3−y)2=(−4−x)2+(3−y)2 ⇒16−8x+x2=16+8x+x2 ⇒16x=0 ⇒x=0 \Rightarrow {\left( {4 - x} \right)^2} + {\left( {3 - y} \right)^2} = {\left( { - 4 - x} \right)^2} + {\left( {3 - y} \right)^2} \\\ \Rightarrow 16 - 8x + {x^2} = 16 + 8x + {x^2} \\\ \Rightarrow 16x = 0 \\\ \Rightarrow x = 0

Also, AB=BCAB = BC
⇒8=(4−x)2+(3−y)2\Rightarrow 8 = \sqrt {{{\left( {4 - x} \right)}^2} + {{\left( {3 - y} \right)}^2}}
Now, squaring both sides

⇒64=(4−x)2+(3−y)2 ⇒64=16−8x+x2+9−6y+y2 ⇒x2+y2−8x−6y+25−64=0 ⇒x2+y2=8x+6y+39 \Rightarrow 64 = {\left( {4 - x} \right)^2} + {\left( {3 - y} \right)^2} \\\ \Rightarrow 64 = 16 - 8x + {x^2} + 9 - 6y + {y^2} \\\ \Rightarrow {x^2} + {y^2} - 8x - 6y + 25 - 64 = 0 \\\ \Rightarrow {x^2} + {y^2} = 8x + 6y + 39

Now, substituting x=0x = 0 in the above equation will give

y2−6y−39=0 ⇒y2−6y+9−9−39=0 ⇒(y−3)2−48=0 ⇒(y−3)2−(43)2=0 ⇒(y−3+43)(y−3−43)=0 {y^2} - 6y - 39 = 0 \\\ \Rightarrow {y^2} - 6y + 9 - 9 - 39 = 0 \\\ \Rightarrow {\left( {y - 3} \right)^2} - 48 = 0 \\\ \Rightarrow {\left( {y - 3} \right)^2} - {\left( {4\sqrt 3 } \right)^2} = 0 \\\ \Rightarrow \left( {y - 3 + 4\sqrt 3 } \right)\left( {y - 3 - 4\sqrt 3 } \right) = 0

Thus, y−3+43=0y - 3 + 4\sqrt 3 = 0 or y−3−43=0y - 3 - 4\sqrt 3 = 0
y=3−43y = 3 - 4\sqrt 3 or y=3+43y = 3 + 4\sqrt 3

So, when the origin lies in the interior, the third vertex will be C(0,3−43)C\left( {0,3 - 4\sqrt 3 } \right).
When the origin lies in the exterior, the third vertex will be C(0,3+43)C\left( {0,3 + 4\sqrt 3 } \right).

Note:
Equilateral triangle:
The triangle which has the length of all three sides the same is called an equilateral triangle. Also, equilateral triangle is equiangular which means all the angles have the same values.