Question

If L.C.M. of $(a, b) = 5^2 \times 3^4$, L.C.M. of $(b, c) = 5^3 \times 3^4$ & L.C.M. of $(c, a) = 5^3 \times 3^4$, then possible ordered triplets of $(a, b, c)$ are k then $\frac{k}{5}$ is equal to

Answer 1

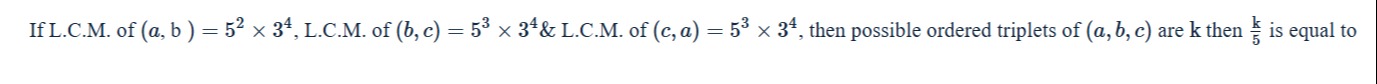
13

Answer 2

Let the prime factorization of $a, b, c$ be:

$a = 5^{x_1} \times 3^{y_1} \times \dots$

$b = 5^{x_2} \times 3^{y_2} \times \dots$

$c = 5^{x_3} \times 3^{y_3} \times \dots$

The L.C.M. of two numbers is found by taking the maximum power of each prime factor present in either number.
The given L.C.M.s are $5^2 \times 3^4$, $5^3 \times 3^4$, and $5^3 \times 3^4$.
This means that $a, b, c$ can only have prime factors 5 and 3. Any other prime factor $p$ would appear in the L.C.M.s with a power greater than or equal to the power of $p$ in $a, b, c$. Since no other prime factors appear in the given L.C.M.s, the exponents of any other prime factor in $a, b, c$ must be 0.
So, we can write:

$a = 5^{x_1} \times 3^{y_1}$

$b = 5^{x_2} \times 3^{y_2}$

$c = 5^{x_3} \times 3^{y_3}$

where $x_i, y_i$ are non-negative integers.

From the given L.C.M. conditions, we have:
For the prime factor 5:
L.C.M.(a, b) = $5^{\max(x_1, x_2)} = 5^2 \implies \max(x_1, x_2) = 2$
L.C.M.(b, c) = $5^{\max(x_2, x_3)} = 5^3 \implies \max(x_2, x_3) = 3$
L.C.M.(c, a) = $5^{\max(x_3, x_1)} = 5^3 \implies \max(x_3, x_1) = 3$

The possible values for $x_1, x_2, x_3$ are non-negative integers. Since the maximum power in the L.C.M.s is 3, the possible values for $x_i$ are $\{0, 1, 2, 3\}$.
From $\max(x_2, x_3) = 3$, at least one of $x_2, x_3$ must be 3.
From $\max(x_3, x_1) = 3$, at least one of $x_3, x_1$ must be 3.

Case 1: $x_3 = 3$.
The conditions become:
$\max(x_1, x_2) = 2$
$\max(x_2, 3) = 3$ (This is true for any $x_2 \le 3$)
$\max(3, x_1) = 3$ (This is true for any $x_1 \le 3$)
So, we need to find the number of pairs $(x_1, x_2)$ such that $\max(x_1, x_2) = 2$, with $x_1, x_2 \in \{0, 1, 2, 3\}$.
Since $\max(x_1, x_2) = 2$, at least one of $x_1$ or $x_2$ must be 2, and neither can be greater than 2.
So, $x_1 \le 2$ and $x_2 \le 2$.
The possible pairs $(x_1, x_2)$ satisfying $\max(x_1, x_2) = 2$ are:

• $x_1 = 2$: $x_2$ can be 0, 1, 2. (3 pairs: (2,0), (2,1), (2,2))
• $x_2 = 2$: $x_1$ can be 0, 1. (2 pairs: (0,2), (1,2) - (2,2) is already counted)
  Total pairs = $3 + 2 = 5$.
  These pairs are (0,2), (1,2), (2,2), (2,1), (2,0).
  So, if $x_3 = 3$, the possible triplets $(x_1, x_2, x_3)$ are (0,2,3), (1,2,3), (2,2,3), (2,1,3), (2,0,3). There are 5 such triplets.

Case 2: $x_3 \ne 3$.
From $\max(x_2, x_3) = 3$, we must have $x_2 = 3$.
From $\max(x_3, x_1) = 3$, we must have $x_1 = 3$.
Now check the first condition: $\max(x_1, x_2) = \max(3, 3) = 3$.
But the condition is $\max(x_1, x_2) = 2$. Since $3 \ne 2$, there are no solutions in this case.

So, there are 5 possible triplets $(x_1, x_2, x_3)$ for the exponents of 5.

For the prime factor 3:
L.C.M.(a, b) = $3^{\max(y_1, y_2)} = 3^4 \implies \max(y_1, y_2) = 4$
L.C.M.(b, c) = $3^{\max(y_2, y_3)} = 3^4 \implies \max(y_2, y_3) = 4$
L.C.M.(c, a) = $3^{\max(y_3, y_1)} = 3^4 \implies \max(y_3, y_1) = 4$

The possible values for $y_1, y_2, y_3$ are non-negative integers. Since the maximum power in the L.C.M.s is 4, the possible values for $y_i$ are $\{0, 1, 2, 3, 4\}$.
From the conditions, at least one exponent in each pair must be 4.
$\max(y_1, y_2) = 4 \implies y_1=4$ or $y_2=4$ (or both)
$\max(y_2, y_3) = 4 \implies y_2=4$ or $y_3=4$ (or both)
$\max(y_3, y_1) = 4 \implies y_3=4$ or $y_1=4$ (or both)

Consider the possibilities for which exponents are equal to 4:

• Exactly one exponent is 4: Not possible. If only $y_1=4$, then $\max(y_2, y_3)=4$ requires $y_2=4$ or $y_3=4$, contradiction.

• Exactly two exponents are 4:

  • $y_1=4, y_2=4, y_3 < 4$: Conditions are $\max(4,4)=4$, $\max(4,y_3)=4$ (true for $y_3 \le 4$), $\max(y_3,4)=4$ (true for $y_3 \le 4$). So, $y_3 \in \{0, 1, 2, 3\}$. There are 4 possibilities.
  • $y_1=4, y_3=4, y_2 < 4$: Conditions are $\max(4,y_2)=4$ (true for $y_2 \le 4$), $\max(y_2,4)=4$ (true for $y_2 \le 4$), $\max(4,4)=4$. So, $y_2 \in \{0, 1, 2, 3\}$. There are 4 possibilities.
  • $y_2=4, y_3=4, y_1 < 4$: Conditions are $\max(y_1,4)=4$ (true for $y_1 \le 4$), $\max(4,4)=4$, $\max(4,y_1)=4$ (true for $y_1 \le 4$). So, $y_1 \in \{0, 1, 2, 3\}$. There are 4 possibilities.
    Total possibilities with exactly two exponents equal to 4 is $4 + 4 + 4 = 12$.

• Exactly three exponents are 4:

  • $y_1=4, y_2=4, y_3=4$: Conditions are $\max(4,4)=4$, $\max(4,4)=4$, $\max(4,4)=4$. This is a valid solution. There is 1 possibility.

Total number of possible triplets $(y_1, y_2, y_3)$ for the exponents of 3 is $12 + 1 = 13$.

The possible ordered triplets $(a, b, c)$ are formed by combining any valid triplet of exponents for 5 with any valid triplet of exponents for 3.
The number of possible triplets $(x_1, x_2, x_3)$ is 5.
The number of possible triplets $(y_1, y_2, y_3)$ is 13.
The total number of possible ordered triplets $(a, b, c)$ is the product of the number of possibilities for the exponents of each prime factor.
$k = (\text{number of possibilities for } (x_1, x_2, x_3)) \times (\text{number of possibilities for } (y_1, y_2, y_3))$
$k = 5 \times 13 = 65$.

The question asks for the value of $\frac{k}{5}$.
$\frac{k}{5} = \frac{65}{5} = 13$.

The final answer is $\boxed{13}$.

Explanation of the solution:

1. Represent $a, b, c$ in terms of their prime factors 5 and 3, with exponents $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ respectively.
2. Use the property of L.C.M. that $\text{L.C.M.}(p_1^{e_1} \dots, p_1^{f_1} \dots) = p_1^{\max(e_1, f_1)} \dots$ to set up equations for the exponents of 5 and 3 separately.
3. For the exponents of 5: $\max(x_1, x_2) = 2$, $\max(x_2, x_3) = 3$, $\max(x_3, x_1) = 3$. Solve for the number of possible integer triplets $(x_1, x_2, x_3)$ where $x_i \in \{0, 1, 2, 3\}$. This gives 5 solutions.
4. For the exponents of 3: $\max(y_1, y_2) = 4$, $\max(y_2, y_3) = 4$, $\max(y_3, y_1) = 4$. Solve for the number of possible integer triplets $(y_1, y_2, y_3)$ where $y_i \in \{0, 1, 2, 3, 4\}$. This gives 13 solutions.
5. The total number of possible ordered triplets $(a, b, c)$ is the product of the number of possibilities for the exponents of each prime factor. $k = 5 \times 13 = 65$.
6. Calculate $\frac{k}{5} = \frac{65}{5} = 13$.

The final answer is $\boxed{13}$.