Question

If l, m, n are the directions cosines of a line, then prove that ${l^2} + {m^2} + {n^2} = 1$. Hence find the directions angles of the line with the x-axis which makes direction angles of ${135^\circ }$ and ${45^\circ }$ with y and z axis respectively.

Answer 1

In this particular type of question assume any variable be the angle of any line with the x, y and z axis respectively, so the cosine of the angle is the direction cosines of the line so use these concepts to reach the solution of the question.

Complete step-by-step answer:
__
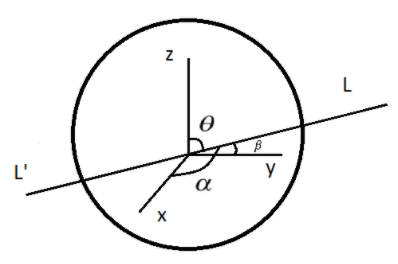
Proof –
Consider a line LL’ which makes an angle $\alpha ,\beta ,\theta$ with the x, y and z axis respectively as shown in the above figure.
It is given that l, m and n are the direction cosines of a line.
Therefore, $l = \cos \alpha$, $m = \cos \beta$ and $n = \cos \theta$
Therefore, ${l^2} + {m^2} + {n^2} = {\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\theta$.................. (1)
Now consider a vector, $\vec p$ be any non-zero vector along the line LL’
Let, $\vec p = {p_1}\hat i + {p_2}\hat j + {p_3}\hat k$.................. (2)
Now since $\hat i$ is a unit vector along the x-axis.
Therefore,
$\vec p.\hat i = \left| {\vec p} \right|.\left| {\hat i} \right|\cos \alpha$....................... (3)
Now from equation (2)
$\Rightarrow \left| {\vec p} \right| = \sqrt {p_1^2 + p_2^2 + p_3^2}$
And
$\left| {\hat i} \right| = 1$
Now from equation (3) we have,
Now from equation (3) we have,
$\Rightarrow \left( {{p_1}\hat i + {p_2}\hat j + {p_3}\hat k} \right).\hat i = \sqrt {p_1^2 + p_2^2 + p_3^2} .\left( 1 \right)\cos \alpha$
$\Rightarrow \left( {{p_1} + 0 + 0} \right) = \sqrt {p_1^2 + p_2^2 + p_3^2} .\left( 1 \right)\cos \alpha$, $\left[ {\because \hat i.\hat i = 1,\hat i.\hat j = 0,\hat i.\hat k = 0} \right]$
$\Rightarrow \cos \alpha = \dfrac{{{p_1}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}$
Similarly,
$\Rightarrow \cos \beta = \dfrac{{{p_2}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}$
$\Rightarrow \cos \theta = \dfrac{{{p_3}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}$
Now substitute these values in equation (1) we have,
$\Rightarrow {l^2} + {m^2} + {n^2} = {\left( {\dfrac{{{p_1}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}} \right)^2} + {\left( {\dfrac{{{p_2}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}} \right)^2} + {\left( {\dfrac{{{p_3}}}{{\sqrt {p_1^2 + p_2^2 + p_3^2} }}} \right)^2}$
$\Rightarrow {l^2} + {m^2} + {n^2} = \left( {\dfrac{{p_1^2}}{{p_1^2 + p_2^2 + p_3^2}}} \right) + \left( {\dfrac{{p_2^2}}{{p_1^2 + p_2^2 + p_3^2}}} \right) + \left( {\dfrac{{p_3^2}}{{p_1^2 + p_2^2 + p_3^2}}} \right)$
$\Rightarrow {l^2} + {m^2} + {n^2} = \left( {\dfrac{{p_1^2 + p_2^2 + p_3^2}}{{p_1^2 + p_2^2 + p_3^2}}} \right) = 1$
Hence proved.
So from equation (1) we have,
$\Rightarrow {\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\theta = 1$
Now it is given that the line makes an angle of ${135^\circ }$ and ${45^\circ }$ with y and z axis respectively.
Therefore, $\beta = {135^\circ },\theta = {45^\circ }$
Now substitute these values in the above equation we have,
$\Rightarrow {\cos ^2}\alpha + {\cos ^2}{135^\circ } + {\cos ^2}{45^\circ } = 1$
$\Rightarrow {\cos ^2}\alpha + {\left( {\dfrac{{ - 1}}{{\sqrt 2 }}} \right)^2} + {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2} = 1$, $\left[ {\because \cos {{135}^\circ } = \dfrac{{ - 1}}{{\sqrt 2 }},\cos {{45}^\circ } = \dfrac{1}{{\sqrt 2 }}} \right]$
Now simplify this we have,
$\Rightarrow {\cos ^2}\alpha + \dfrac{1}{2} + \dfrac{1}{2} = 1$
$\Rightarrow {\cos ^2}\alpha + 1 = 1$
$\Rightarrow {\cos ^2}\alpha = 0$
$\Rightarrow \cos \alpha = 0$
$\Rightarrow \cos \alpha = \cos {90^\circ }$
$\Rightarrow \alpha = {90^\circ }$
So the line makes an angle 90 degrees with the x-axis.
So this is the required answer.

Note: Whenever we face such types of questions the key concept we have to remember is that always recall the values of the standard trigonometric angles which is stated above, then simply substitute the values in the equation and simplify as above we will get the required direction angle of line with the x-axis.