Question

If $l,m,n$ are direction cosines of a straight line then prove that ${l^2} + {m^2} + {n^2} = 1$.

Answer 1

Find the dimensions of the lines joining the $x,y$ and $z$ axes, to use it further into the equation formed by solving the equations of direction cosines using the distance formula. We use simple coordinates to represent the values of the given angles and the points.

Complete step-by-step solution:

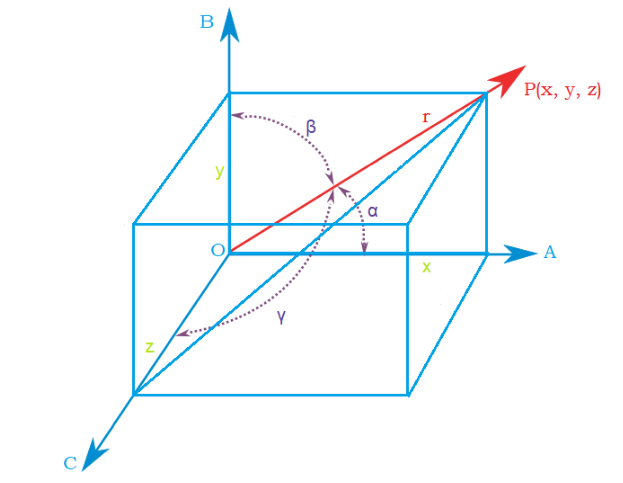
Let $O$ be the origin and $OP$ be a line Which has the direction cosines as $l,m,n$.
Let the coordinates of $P$ be $(x,y,z)$.
Let the length of the line $OP$ be $r$.
The coordinates of origin $O = (0,0,0)$.
Using the three- coordinates distance formula:
$OP = \sqrt {{{(x - 0)}^2} + {{(y - 0)}^2} + {{(z - 0)}^2}}$
$\Rightarrow OP = \sqrt {{x^2} + {y^2} + {z^2}}$
Squaring on both sides of the equation, we get:
$O{P^2} = {x^2} + {y^2} + {z^2}$
Now, $OP = r$
Substituting $OP = r$ in the above equation
${r^2} = {x^2} + {y^2} + {z^2} - - - - \left( 1 \right)$
$PA,PB,PC$ are joined perpendicularly on the coordinate axes such that:
$OA = x$, $OB = y$, $OC = z$
The angles between the following lines with the origin are as follows:
$\angle POA = \alpha$, $\angle POB = \beta$, $\angle POC = \gamma$
Now,
Given direction cosines are $l,m,n$.
$\cos \alpha = l$, $\cos \beta = m$, $\cos \gamma = n$
Let us consider the $\vartriangle AOP$,
$\cos \alpha = \dfrac{x}{r}$
By using $\cos \alpha = l$ we get,
$\Rightarrow l = \dfrac{x}{r}$
Hence,
$\Rightarrow x = lr$
Squaring on both sides:
${x^2} = {l^2}{r^2} - - - - \left( 2 \right)$
Similarly,
$\cos \beta = \dfrac{y}{r}$
By using $\cos \beta = m$ we get,
$\Rightarrow m = \dfrac{y}{r}$
Hence,
$\Rightarrow y = mr$
Squaring on both sides:
${y^2} = {m^2}{r^2} - - - - \left( 3 \right)$
And,
$\cos \gamma = \dfrac{z}{r}$
By using $\cos \gamma = n$ we get,
$\Rightarrow n = \dfrac{z}{r}$
Hence,
$\Rightarrow z = nr$
Squaring on both sides:
${z^2} = {n^2}{r^2} - - - - \left( 4 \right)$
$\therefore {\text{ }}x = lr$, $y = mr$, $z = nr$
Adding $2,{\text{ }}3,{\text{ }}4$, we get:
${x^2} + {y^2} + {z^2} = {l^2}{r^2} + {m^2}{r^2} + {n^2}{r^2}$
Taking out the common terms
$\Rightarrow {x^2} + {y^2} + {z^2} = ({l^2} + {m^2} + {n^2}){r^2}$
From equation $1$:
$\Rightarrow {r^2} = ({l^2} + {m^2} + {n^2}){r^2}$
Cancelling the common terms on both the sides, that is diving both the sides using ${r^2}$
${l^2} + {m^2} + {n^2} = 1$
Hence proved

Note: In analytic geometry, the direction cosines (or directional cosines) of a vector are the cosines of the angles between the vector and the three coordinate axes. Equivalently, they are the contributions of each component of the basis to a unit vector in that direction. Direction cosines are an analogous extension of the usual notion of slope to higher dimensions.