Question
Question: If $L = \lim_{x\to\frac{\pi}{2}} \frac{\sqrt{1 + \cot x} - \sqrt{1 + \cos x}}{(\pi - 2x)^3}$, then ...
If
L=limx→2π(π−2x)31+cotx−1+cosx, then 96 L is _______ .
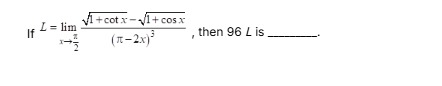
3
Solution
To evaluate the limit L=limx→2π(π−2x)31+cotx−1+cosx, we first observe that as x→2π, the expression is of the indeterminate form 00.
Let's make a substitution to simplify the limit. Let x=2π+h. As x→2π, h→0.
Now, substitute x=2π+h into the expression:
-
Denominator: (π−2x)3=(π−2(2π+h))3=(π−π−2h)3=(−2h)3=−8h3.
-
Numerator: cotx=cot(2π+h)=−tanh. cosx=cos(2π+h)=−sinh. So, the numerator becomes 1−tanh−1−sinh.
The limit expression transforms to: L=limh→0−8h31−tanh−1−sinh
To simplify the numerator, multiply and divide by its conjugate: L=limh→0−8h3(1−tanh+1−sinh)(1−tanh−1−sinh)(1−tanh+1−sinh) L=limh→0−8h3(1−tanh+1−sinh)(1−tanh)−(1−sinh) L=limh→0−8h3(1−tanh+1−sinh)sinh−tanh
As h→0, the term 1−tanh+1−sinh approaches 1−0+1−0=1+1=2. So, we can write: L=−8×21limh→0h3sinh−tanh L=−161limh→0h3sinh−coshsinh L=−161limh→0h3sinh(1−cosh1) L=−161limh→0h3sinh(coshcosh−1)
Now, rearrange the terms to use standard limits: L=−161limh→0(hsinh×h2cosh−1×cosh1)
We know the following standard limits:
- limh→0hsinh=1
- limh→0h2cosh−1=−21
- limh→0cosh1=cos01=11=1
Substitute these values into the expression for L: L=−161×(1)×(−21)×(1) L=−161×(−21) L=321
The question asks for the value of 96L. 96L=96×321=3.
The final answer is 3.
Explanation of the solution:
- Substitute x=2π+h to transform the limit as h→0.
- Simplify trigonometric terms: cot(2π+h)=−tanh and cos(2π+h)=−sinh.
- Rationalize the numerator by multiplying by its conjugate.
- Factor out sinh from the numerator and rearrange terms to identify standard limits: limh→0hsinh, limh→0h2cosh−1, and limh→0cosh1.
- Substitute the values of these standard limits to find L.
- Calculate 96L.
