Question

If ${l_1},{\text{ }}{m_1},{\text{ }}{n_1},$and ${l_2},{\text{ }}{m_2},{\text{ }}{n_2},$ be the DC’s of two concurrent lines, the direction cosines of the line bisecting the angles between them are proportional to
A) ${l_1}{l_2},{\text{ }}{m_1}{m_2},{\text{ }}{n_1}{n_2}$
B) ${l_1}{m_2},{\text{ }}{l_1}{n_2},{\text{ }}{l_1}{n_3}$
C) ${l_1} + {\text{ }}{l_2}{,_{}}{m_1} + {\text{ }}{m_2},{\text{ }}{n_1} + {\text{ }}{n_2}$
D) None of these

Answer 1

Hint : In the question we are given, the lines are concurrent and direction cosines are also given. We will start with drawing a figure first, and then using the given information we will solve accordingly.

Complete step-by-step answer :
Let us first draw a figure, in it let the two concurrent lines be OA and OB, where O is the meeting point and C is the midpoint of A and B. And let the direction cosines of OA $=$ ${l_1},{\text{ }}{m_1},{\text{ }}{n_1},$ and direction cosines of OB $=$ ${l_2},{\text{ }}{m_2},{\text{ }}{n_2},$

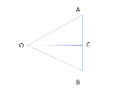
Now, since OA and OB are concurrent lines, so we can take, $OA{\text{ }} = {\text{ }}OB{\text{ }} = {\text{ }}r$
Then, C is the midpoint of AB. Then, OC is the bisector of the $\angle AOB.$
Now, with that we will get the coordinates of A and B which are $\left( {{l_1}r,{m_1}r,{n_1}r} \right)$ and $\left( {{l_2}r,{m_2}r,{n_2}r} \right)$respectively.
So, we will get the coordinates of C which are,
$\frac{{({l_1} + {l_2})r}}{2},\frac{{({m_1} + {m_2})r}}{2},\frac{{({n_1} + {n_2})r}}{2}$
So, the direction cosines of OC become proportional to ${l_1} + {\text{ }}{l_2}{,_{}}{m_1} + {\text{ }}{m_2},{\text{ }}{n_1} + {\text{ }}{n_2}$
Thus, option (C), ${l_1} + {\text{ }}{l_2}{,_{}}{m_1} + {\text{ }}{m_2},{\text{ }}{n_1} + {\text{ }}{n_2}$ is correct.
So, the correct answer is “Option C”.

Note : The lines which pass through the same point and are equal, are called concurrent lines. Direction cosines of a line are the cosines of the angle made by the line with the positive direction of the coordinate axes.