Question

If inverse trigonometric function is given as \cos \left\\{ {{{\tan }^{ - 1}}\left( {\sin \left( {{{\cot }^{ - 1}}x} \right)} \right)} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}. Find the value of $a + b + c$.
${\text{A}}{\text{. 3}} \\\ {\text{B}}{\text{. 4}} \\\ {\text{C}}{\text{. 5}} \\\ {\text{D}}{\text{. 6}} \\\$

Answer 1

Hint: Here, we will be converting the inverse trigonometric functions into a trigonometric function next to the inverse trigonometric function so that they are just left with the angle.

Complete step-by-step solution:
Given, \cos \left\\{ {{{\tan }^{ - 1}}\left( {\sin \left( {{{\cot }^{ - 1}}x} \right)} \right)} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}{\text{ }} \to {\text{(1)}}
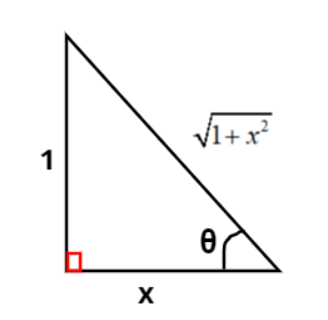
Consider $\theta = {\cot ^{ - 1}}x \Rightarrow \cot \theta = x$, the diagram corresponding to this function is shown in Figure 1.

Equation (1), becomes
\cos \left\\{ {{{\tan }^{ - 1}}\left( {\sin \theta } \right)} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}{\text{ }} \to {\text{(2)}}
Here we will convert this inverse cotangent trigonometric function into inverse sine trigonometric function.
$\theta = {\cot ^{ - 1}}x \Rightarrow \cot \theta = \dfrac{x}{1} = \dfrac{{{\text{Base}}}}{{{\text{Perpendicular}}}}$
$\Rightarrow {\text{Base}} = x$ and ${\text{Perpendicular}} = 1$
As according to Pythagoras theorem in a right angled triangle, we can write
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2}{\text{ + }}{\left( {{\text{Base}}} \right)^2} \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {1^2} + {x^2} \Rightarrow {\text{Hypotenuse}} = \sqrt {1 + {x^2}}$ As, $\sin \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} = \dfrac{1}{{\sqrt {1 + {x^2}} }} \Rightarrow \theta = {\sin ^{ - 1}}\left[ {\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right]$
Hence equation (2) becomes
\cos \left\\{ {{{\tan }^{ - 1}}\left( {\sin \left( {{{\sin }^{ - 1}}\left[ {\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right]} \right)} \right)} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}
We know that $\sin \left( {{{\sin }^{ - 1}}\beta } \right) = \beta$, the above equation becomes
\Rightarrow \cos \left\\{ {{{\tan }^{ - 1}}\left( {\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right)} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}{\text{ }} \to {\text{(3)}}
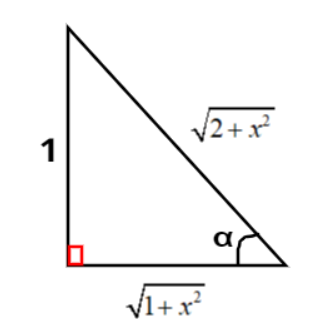
Now let ${\tan ^{ - 1}}\left( {\dfrac{1}{{\sqrt {1 + {x^2}} }}} \right) = \alpha \Rightarrow \tan \alpha = \dfrac{1}{{\sqrt {1 + {x^2}} }} = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$, the diagram corresponding to this function is shown in Figure 2.

Equation (3) becomes,
$\Rightarrow \cos \alpha = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}{\text{ }} \to {\text{(4)}}$
Here we will convert this inverse tangent trigonometric function into inverse cosine trigonometric function.
$\Rightarrow {\text{Perpendicular}} = 1$ and ${\text{Base}} = \sqrt {1 + {x^2}}$
Again according to Pythagoras theorem in a right angled triangle, we can write
${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2}{\text{ + }}{\left( {{\text{Base}}} \right)^2} \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {1^2} + {\left( {\sqrt {1 + {x^2}} } \right)^2} = 1 + 1 + {x^2} \\\ \Rightarrow {\text{Hypotenuse}} = \sqrt {2 + {x^2}} \\\$
As, $\cos \alpha = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{{\sqrt {1 + {x^2}} }}{{\sqrt {2 + {x^2}} }} = \sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}} \Rightarrow \alpha = {\cos ^{ - 1}}\left[ {\sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}} } \right]$
Hence equation (4) becomes
\Rightarrow \cos \left\\{ {{{\cos }^{ - 1}}\left[ {\sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}} } \right]} \right\\} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}
We know that $\cos \left( {{{\cos }^{ - 1}}\beta } \right) = \beta$, the above equation becomes
$\Rightarrow \sqrt {\dfrac{{1 + {x^2}}}{{2 + {x^2}}}} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}} \\\ \Rightarrow {\left( {\dfrac{{{x^2} + 1}}{{{x^2} + 2}}} \right)^{\dfrac{1}{2}}} = {\left( {\dfrac{{{x^a} + 1}}{{{x^b} + 2}}} \right)^{\dfrac{1}{c}}}{\text{ }} \to {\text{(5)}} \\\$
On comparing equation (5), the values of the unknowns obtained are $a = 2$, $b = 2$ and $c = 2$
Therefore, $a + b + c = 2 + 2 + 2 = 6$
Hence, option D is correct.

Note: In these types of problems, conversion of trigonometric functions is required so that the next trigonometric function is eliminated with the inverse trigonometric function.