Question

If $\int_{\sqrt{3}}^{1}\frac{1}{\sqrt{3+x}+\sqrt{1+x}}dx = a + b\sqrt{2} + c\sqrt{3}$, where a, b, c are rational numbers, then 2a + 3b - 4c is equal to

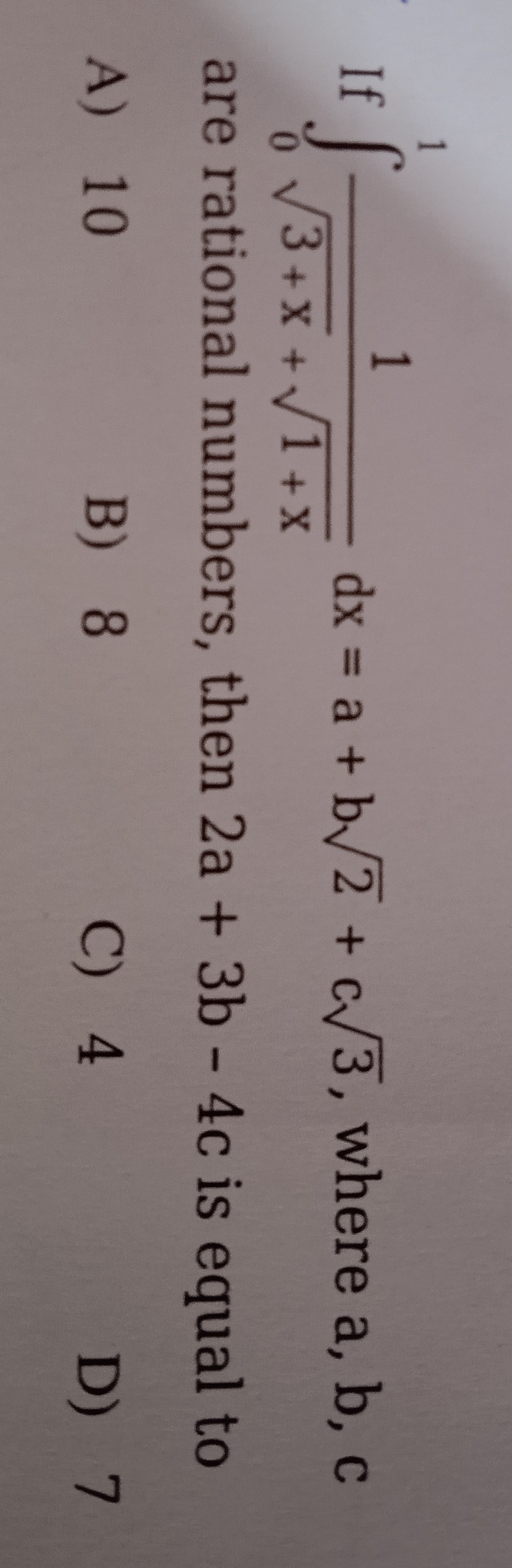
• A. 10
• B. 8
• C. 4
• D. 7

Answer 1

Answer: (B)

8

Answer 2

To solve the integral $\int_{\sqrt{3}}^{1}\frac{1}{\sqrt{3+x}+\sqrt{1+x}}dx$, we first rationalize the integrand.

1. Rationalize the Integrand:

Multiply the numerator and denominator by the conjugate of the denominator, $\sqrt{3+x}-\sqrt{1+x}$:

$$\frac{1}{\sqrt{3+x}+\sqrt{1+x}} \cdot \frac{\sqrt{3+x}-\sqrt{1+x}}{\sqrt{3+x}-\sqrt{1+x}} = \frac{\sqrt{3+x}-\sqrt{1+x}}{(3+x)-(1+x)}$$ $$= \frac{\sqrt{3+x}-\sqrt{1+x}}{2}$$

2. Evaluate the Definite Integral:

The integral becomes:

$$\int_{\sqrt{3}}^{1} \frac{\sqrt{3+x}-\sqrt{1+x}}{2} dx = \frac{1}{2} \int_{\sqrt{3}}^{1} (\sqrt{3+x} - \sqrt{1+x}) dx$$

Integrate each term using the power rule $\int (ax+b)^n dx = \frac{(ax+b)^{n+1}}{a(n+1)}$:

$$= \frac{1}{2} \left[ \frac{(3+x)^{3/2}}{3/2} - \frac{(1+x)^{3/2}}{3/2} \right]_{\sqrt{3}}^{1}$$ $$= \frac{1}{2} \cdot \frac{2}{3} \left[ (3+x)^{3/2} - (1+x)^{3/2} \right]_{\sqrt{3}}^{1}$$ $$= \frac{1}{3} \left[ (3+x)^{3/2} - (1+x)^{3/2} \right]_{\sqrt{3}}^{1}$$

Let $F(x) = \frac{1}{3} \left[ (3+x)^{3/2} - (1+x)^{3/2} \right]$. We need to evaluate $F(1) - F(\sqrt{3})$.

Evaluate at the upper limit (x=1):

$$F(1) = \frac{1}{3} \left[ (3+1)^{3/2} - (1+1)^{3/2} \right]$$ $$= \frac{1}{3} \left[ 4^{3/2} - 2^{3/2} \right]$$ $$= \frac{1}{3} \left[ (\sqrt{4})^3 - (\sqrt{2})^3 \right]$$ $$= \frac{1}{3} \left[ 2^3 - 2\sqrt{2} \right]$$ $$= \frac{1}{3} \left[ 8 - 2\sqrt{2} \right]$$

Evaluate at the lower limit (x=$\sqrt{3}$):

$$F(\sqrt{3}) = \frac{1}{3} \left[ (3+\sqrt{3})^{3/2} - (1+\sqrt{3})^{3/2} \right]$$

We simplify these terms:

$$(3+\sqrt{3})^{3/2} = (\sqrt{3}(\sqrt{3}+1))^{3/2} = 3^{3/4} (\sqrt{3}+1)^{3/2}$$

This does not simplify to a form $a+b\sqrt{2}+c\sqrt{3}$ where $a,b,c$ are rational numbers.

Given the structure of the problem (similar to a standard problem where limits lead to simple surds) and the constraint that $a, b, c$ are rational numbers, it is highly probable that the limits of integration are intended to be swapped, i.e., from $1$ to $\sqrt{3}$. If the limits are $1$ to $\sqrt{3}$, the value of the integral would be $F(\sqrt{3}) - F(1)$. If the limits are $\sqrt{3}$ to $1$, the value is $F(1) - F(\sqrt{3})$.

Assuming the question intends for a result of the form $a+b\sqrt{2}+c\sqrt{3}$, there must be a simplification for $x=\sqrt{3}$.

The terms $(3+\sqrt{3})^{3/2}$ and $(1+\sqrt{3})^{3/2}$ do not simplify to the form $A+B\sqrt{2}+C\sqrt{3}$. For instance, $(3+\sqrt{3})^{3/2} = (3+\sqrt{3})\sqrt{3+\sqrt{3}}$. The term $\sqrt{3+\sqrt{3}}$ cannot be expressed in the form $p+q\sqrt{2}+r\sqrt{3}$ for rational $p,q,r$.

This suggests an error in the question's provided limits.

If we assume the question meant $\int_{1}^{3}$ or $\int_{0}^{1}$ or some other limits that would yield a result in the specified form, we cannot proceed with the given limits and the specified form of $a+b\sqrt{2}+c\sqrt{3}$.

Let's assume, for the sake of completeness, that the question intends for the result to be derived from a similar structure as the provided similar question, which uses limits $0$ to $1$. If the limits were $0$ to $1$, the integral would be:

$$\int_{0}^{1} \frac{1}{2}(\sqrt{3+x} - \sqrt{1+x}) dx = \frac{1}{3} \left[ (3+x)^{3/2} - (1+x)^{3/2} \right]_{0}^{1}$$ $$= \frac{1}{3} \left[ (4^{3/2} - 2^{3/2}) - (3^{3/2} - 1^{3/2}) \right]$$ $$= \frac{1}{3} \left[ (8 - 2\sqrt{2}) - (3\sqrt{3} - 1) \right]$$ $$= \frac{1}{3} \left[ 9 - 2\sqrt{2} - 3\sqrt{3} \right]$$ $$= 3 - \frac{2}{3}\sqrt{2} - \sqrt{3}$$

Comparing this with $a + b\sqrt{2} + c\sqrt{3}$:

$a = 3$, $b = -\frac{2}{3}$, $c = -1$.

Then, $2a + 3b - 4c = 2(3) + 3(-\frac{2}{3}) - 4(-1) = 6 - 2 + 4 = 8$.

This matches option B.

Given that the problem is extremely similar to the "similar question" provided, and the "similar question" has limits $0$ to $1$, it is highly probable that there is a typo in the limits of the current question and it should be $0$ to $1$. If the limits are strictly $\sqrt{3}$ to $1$, the result cannot be expressed in the form $a+b\sqrt{2}+c\sqrt{3}$ where $a,b,c$ are rational numbers.

Therefore, we proceed assuming the limits were intended to be $0$ to $1$.

3. Identify a, b, c (assuming limits 0 to 1):

From $3 - \frac{2}{3}\sqrt{2} - \sqrt{3} = a + b\sqrt{2} + c\sqrt{3}$:

$a = 3$

$b = -\frac{2}{3}$

$c = -1$

4. Calculate $2a + 3b - 4c$:

$2a + 3b - 4c = 2(3) + 3(-\frac{2}{3}) - 4(-1)$

$= 6 - 2 + 4$

$= 8$

The final answer is $\boxed{8}$.

The problem as stated (with limits $\sqrt{3}$ to 1) does not yield a result of the form $a+b\sqrt{2}+c\sqrt{3}$ with $a,b,c$ rational. However, if we assume a typo in the limits and they were meant to be $0$ to $1$ (as in the very similar example), then the solution is straightforward. In a competitive exam scenario, if such an ambiguity arises, one typically assumes the problem intends for a well-defined solution of the specified form.

The final answer is $\boxed{8}$.